Принципи побудови багатофакторних індексних моделей
Андрієнко В.Ю.
Побудова багатофакторних індексних моделей повинна ґрунтуватися на принципах, що випливають з об’єктивних особливостей взаємозв’язку між явищами. Це стосується, насамперед, первісної стадії аналізу – складання вихідних моделей, що відбивають зв’язок між результативними і факторними показниками.
У загальному вигляді індексний аналіз покликаний дати кількісну оцінку функціональних причинно-наслідкових зв’язків між економічними явищами. об’єктивність і практична цінність такої оцінки залежить, по-перше, від правильного трактування сутності взаємозалежних явищ, по-друге, від повноти обліку особливостей даного взаємозв’язку.
Почнемо з факторних моделей, результативним показником яких виступає об’ємний показник. Основою утворення багатофакторних моделей об’ємного показника слугують двофакторні моделі, що містять кількісний і якісний фактори. Побудова двофакторних моделей відбувається, як правило, шляхом розкладання показника на два його фактори, один з яких у свою чергу може бути розчленованим на його субфактори.
Даний процес не може бути механічним, він повинен спиратися на певні методологічні принципи. Один з них – необхідність визначення факторів у часі. Аналіз свідчить, що в умовах тимчасового розвитку факторів кожен наступний у часі фактор повинен виступати як результат попередніх йому факторів, а не навпаки. Найпростішою формою такого розвитку факторів є моделі, що будуються на чисто тимчасовому характері взаємозв’язків. Наприклад, обсяг виробництва продукції за рік можна відобразити такими двофакторними моделями:
а) Q = R × Q/r;
б) Q = D – Q/D;
в) Q = T' × Q/T' ,
де r – кількість відпрацьованих за рік людино-годин усіма робітниками; D – кількість відпрацьованих за рік людино-днів усіма робітниками; T' – середньорічна чисельність робітників. Відносні показники Q/r, Q/D i Q/T' відображають відповідно середньогодинну, середньоденну і середньорічну продуктивність праці.
Виходячи з того, що середньоденна продуктивність складається із середньогодинної, а річна – з середньоденної, наведені моделі деталізуються у такий спосіб:
Q/D = Q/r – r/D; Q/T' = Q/D × D/T' = Q/r × r/D × D/T',
де r/D i D/T( – відповідно тривалість робочого дня (у годинах) і тривалість робочого року (у днях).
Підставляючи у формулу розгорнуте значення Q/T', одержимо чотирифакторну модель обсягу продукції
Q = T' × Q/r × rl × D/T'.
Відмітимо, що хоча математично припустимі й інші способи відображення одних факторів через інші, але логічний хід розвитку подій диктує саме приведений порядок їхнього розгортання в багатофакторній моделі.
Наступний принцип утворення багатофакторних індексних моделей – поширення факторної залежності одних результативних показників на інші, похідні від перших. Наприклад, факторна модель обсягу виробництва може служити вихідною базою для побудови багатофакторних моделей аналізу багатьох похідних від нього економічних категорій. Припустимо, потрібно побудувати багатофакторні моделі таких безпосередньо залежних від нього категорій, як обсяг реалізованої продукції R, чи фонд заробітної плати робітників Ф. Безпосередній зв’язок даних категорій з обсягом виробництва продукції можна відобразити в такий спосіб:
R = Q × R/Q; Ф = Q × Ф/Q,
де R/Q – питома вага реалізованої продукції в обсязі валової продукції (чи так званий коефіцієнт реалізації); Ф/Q – витрати заробітної плати на одиницю валової продукції (своєрідний показник оплати праці за вартісну одиницю продукції).
Підставляючи у щойно наведені формули розгорнуте значення Q, одержимо багатофакторні моделі аналізу обсягу реалізованої продукції і фонду заробітної плати робітників:
R = T' × Q/r × r/D × D/T' × R/Q;
Ф = T' × Q/r × r/D × D/T' × Ф/Q.
Дані рівняння ґрунтуються на припущенні, що фактори, які впливають на обсяг виробництва, залишаються в силі і стосовно похідних від нього категорій. У зв’язку з цим можна будувати багатофакторні моделі і для якісних показників. Наприклад, залежність середньої заробітної плати робітників від визначальних її факторів можна передати формулою:
ф/T' = Ф/Q × Q/r × r/D × D/T'.
Тут досить чітко визначена функціональна залежність середньої заробітної плати робітників від факторів, що залежать безпосередньо від робітників, зокрема, від рівня годинної продуктивності їхньої праці і від повноти використання ними робочого часу, а також зовнішнього фактора – питомої ваги витрат заробітної плати у вартісній одиниці продукції. Варто відзначити, що ігнорування тимчасової субординації факторів призводить до утворення формальних моделей. У цьому легко переконатися, побудувавши, наприклад, модель "залежності" обсягу виробленої продукції від обсягу реалізованої продукції, модель "залежності" продуктивності праці від середньої заробітної плати тощо.
Принцип поширення факторної залежності одних показників на інші, похідні від перших, є багатоступеневим. Якщо, наприклад, на показник реалізованої продукції поширюються фактори, що впливають на обсяг виробленої продукції, то ці ж фактори залишаються в силі і стосовно всіх категорій, похідних від обсягу реалізації.
Так, задамося метою деталізувати відому двофакторну модель прибутку m: m = F × m/F, де с – обсяг виробничих фондів; m/F – рентабельність виробничих фондів.
Багато дослідників вважають фондорентабельність результативним показником, факторами якого нібито є прибуток і обсяг виробничих фондів. У дійсності ж фондорентабельність – фактор прибутку, тому що прибуток "створюється" виробничими фондами і властивої їм фондорентабельності, подібно тому, як виробничими фондами і властивою їм фондовіддачею "створюється" обсяг продукції.
Для досягнення поставленої мети необхідна, як мінімум, ще одна двофакторна модель прибутку. Її нескладно побудувати, якщо врахувати, що прибуток залежить насамперед від обсягу реалізованої продукції і її рентабельності. Залежність прибутку від обсягу реалізованої продукції R можна відобразити формулою:
m = R × m/R,
де m/R – питома вага прибутку в обсягах реалізації, тобто рентабельність одиниці реалізованої продукції.
Фондорентабельність утворюється тільки після реалізації продукції, тому вона є наслідком, а реалізація продукції – причиною, тобто формула визначення фондорентабельності буде мати вигляд:
m/F = m/R × R/F.
З огляду на той факт, що реалізації продукції передує її виробництво, щойно наведену формулу можна представити так:
m/F = m/R × R/Q × Q/F.
Логічність наведеної формули не викликає сумніву, тому що рентабельність фондів дійсно залежить від рентабельності одиниці реалізованої продукції m/R, на яку, у свою чергу, впливає коефіцієнт реалізації виробленої продукції R/Q, а на останній – рівень використання виробничих фондів, тобто фондовіддача Q/F.
Підставляючи у модель прибутку розгорнуте значення показника фондорентабельності, одержимо чотирифакторну модель аналізу прибутку:
m = F × m/R × R/Q × Q/F.
Сутність цих залежностей залишиться економічно осмисленою і справедливою, якщо обсяг прибутку розглядати, скажімо, як категорію, похідну від загальних витрат на виробництво (іншими словами, як фабрично-заводську собівартість S) і рівня віддачі загальних витрат (тобто рентабельності продукції – m/S):
m = S × m/S.
Для цього випадку за аналогією з наведеною моделлю прибутку можна скласти і наступну модель факторного аналізу прибутку;
m = S × m/R × R/Q × Q/S,
де Q/S – вихід продукції на одиницю виробничих витрат (показник окупності витрат). У загальному вигляді така модель відбиває залежність маси прибутку від розмірів первісних вкладень у виробництво S і наступних якісних показників виробничо-фінансової діяльності.
Викладене ще раз переконує в тому, що логічність факторних залежностей зберігається незмінно, якщо вони будуються відповідно до природного ходу розвитку подій. Варто цим положенням знехтувати, і факторний аналіз направляється в помилковому напрямі. Припустимо, у моделі не фондорентабельність була б залежною від рентабельності реалізованої продукції m/R, а навпаки. Тоді одержали б економічно некоректну залежність:
m/R = m/F × F/R,
де F/R – показник фондомісткості реалізованої продукції, зростання якого виступає наче позитивним моментом стосовно рентабельності продукції, хоча в дійсності це момент негативний.
Таким чином, у причинно-наслідкових зв’язках з яскраво вираженим чергуванням явищ у часі деталізація моделей повинна відбуватися шляхом розгортання наступних факторів через попередні. Однак, такої черговості явищ в економічній практиці часто не існує, вірніше, явища розташовуються відносно один до одного і послідовно, і паралельно. Типовим прикладом паралельного існування факторів є розглянута нами залежність обсягу виробництва від одночасно функціонуючих факторів – чисельності робочих і виробничих фондів, а також похідних від них категорій – продуктивності праці і фондовіддачі. Разом з тим раніше було показано, що в таких випадках правомірна зворотна деталізація якісних факторів, наприклад, відображення фактора продуктивності праці через фондовіддачу Q/T = Q/F × F/T, і навпаки, – фондовіддачі через продуктивність праці Q/F = Q/T × T/F. У зв’язку з цим виникають ще два принципові питання.
Перше: де знайти фактори, необхідні для деталізації якісних показників, щоб вони отримувались майже автоматично?
Для цього доцільно утворити ряд двофакторних моделей об’ємного показника, фактори якого не зв’язані між собою тимчасовою субординацією. Наприклад, величина приросту ваги худоби на відгодівлі (M) залежить від двох основних факторів – чисельності відгодовуваного поголів’я (П) та наявності кормів (К). Ці фактори присутні одночасно, тобто паралельно. На цій підставі можна побудувати дві паралельно існуючі моделі факторної залежності обсягу виробництва м’яса:
а) М = П × М/П;
б) М = К × М/К,
де М/П – середня вага відгодовуваної худоби (її продуктивність); М/К – вихід м’яса на одиницю корму (показник поживності кормів).
Користуючись вихідними моделями а і б, факторну модель якісних показників М/П чи М/К можна конструювати механічно. Для цього досить один з них обрати результативним, тоді другий виявиться факторним, до якого необхідно додати ще один фактор, який доповнює модель до математичної рівності, наприклад:
М/П = М/К × К/П; М/К = М/П × П/К,
де К/П – кількість корму, що приходиться на одну голову худоби (рівень відгодівлі худоби); П/К – зворотний йому показник (кількість худоби, що приходиться на одиницю корму).
Якщо коректні за економічним змістом вихідні моделі, то неминуче забезпечуються і логічність похідних моделей. Так, середня вага (продуктивність) відгодовуваної худоби М/П дійсно залежить від рівня відгодівлі К/П та поживності (якості) кормів М/К. У свою чергу величина приросту ваги на одиницю корму М/К залежить від чисельності поголів’я, що приходиться на одиницю кормів П/К і продуктивності кожної голови худоби М/П.
Щоб уникнути можливих непорозумінь у трактуванні причинно-наслідкових залежностей, слід мати на увазі певну еластичність у смислових відтінках одного і того ж економічного показника. Так, у досліджуваних залежностях показник М/К, будучи факторним стосовно М/П, розглядається як показник поживності (якості) кормів, а будучи результативним – як величина приросту ваги на одиницю корму. В прямому розумінні він дійсно відбиває рівень приросту ваги на одиницю корму, але в причинно-наслідковому аспекті його можна розглядати як показник поживності (якості) кормів, тому що чим більший вихід приросту ваги на одиницю корму, тим вища якість (поживність) останнього.
Друге питання: яким чином можна переконатися, що дані фактори дійсно паралельні, а не послідовні або які-небудь інші?
Правильне рішення тут можливе на основі глибокого якісного аналізу взаємозв’язків між явищами. Головна ознака факторних показників – їхній безпосередній вплив на результативний показник. В зв’язку з цим паралельні фактори повинні характеризуватися одночасністю безпосереднього впливу та природною спільністю їхнього поєднання в процесі "становлення" результативного показника. Найбільш типова ознака такої спільності – можливість і допустимість за певних умов деякої взаємозаміни факторів. Наприклад, поголів’я худоби на відгодівлі може скоротитися, але це скорочення можна компенсувати зростанням його продуктивності шляхом збільшення кількості і підвищення якості кормів.
Аналогічна взаємозаміна (у визначених межах) можлива між масою живої та уречевленої праці, що приймають участь у виробництві. Так, на основі росту механізації й автоматизації виробництва відбувається вивільнення робочої сили, або недостатня кількість засобів праці частково може бути замінена живою працею.
Відсутність взаємозамінності між факторами, якщо вони нерозривні як елементи єдиного виробничого процесу, свідчить про їхню економічну різнорідність, що обумовлена або різною значимістю факторів стосовно результативного показника, або присутньою субординацією факторів у часі.
При аналізі факторів особливо важливо враховувати їх сутнісну спорідненість чи відмінність. Відомо, наприклад, що в процесі виробництва беруть участь три нерозривних його елементи: засоби праці, предмети праці і робоча сила. У зв’язку з цим приведемо три відомі моделі факторної залежності обсягу виробництва від перерахованих елементів:
Q = T × w;
Q = F × f;
Q = N × n,
де T – чисельність робочої сили; F – обсяг основних виробничих фондів; N – обсяг предметів праці (сировини, палива, тощо); w, f, n – відповідні цим факторам якісні показники: продуктивність праці, фондовіддача, вихід продукції на одиницю предметів праці (показник, зворотний показнику матеріалоємності продукції).
Перші два кількісних фактори (T і F) такі, що підлягають взаємозаміні. Вони паралельні й одноякісні з погляду впливу на результативний показник, тому їхні якісні показники (w i f) можуть деталізуватись за принципом зворотності зв’язку, в основі якої лежить принцип взаємозаміни кількісних факторів. Третій кількісний фактор (N) не підлягає взаємозаміні першими двома, оскільки сировина (матеріали) не можуть бути замінені виробничим устаткуванням чи робочою силою. Отже, хоч він і існує паралельно з першими двома факторами, але якісно відрізняється від них. Це розходження проявляється подвійно. По-перше, у зв’язку з різною активністю при участі в продуктивному процесі: знаряддя праці і робоча сила створюють продукт безпосередньо, роль же предметів праці в цьому процесі пасивна. По-друге, предмети праці, що складають речовинну субстанцію створюваного продукту, піддаються переробці з боку засобів праці і робочої сили, тобто сприймають на себе продукуючий вплив активних факторів і в цьому відношенні стають первинним елементом виробництва в часовому аспекті.
Подібний аналіз особливостей функціонування факторів з огляду на їх якісну спорідненість щодо характеру впливу на результативний показник та одночасної субординації між ними дозволяють визначити певний порядок і послідовність у розгортанні факторних моделей. Виходячи, наприклад, з того, що два фактори в даному випадку одноякісні й одномоментні за їх впливом на продукуючу діяльність, а третій трохи зрушений у часовому аспекті в минуле і відрізняється від них характером впливу на результативний показник, визначаємо, що можлива деталізація якісних показників, похідних тільки від перших двох факторів, тобто показників продуктивності праці і фондовіддачі.
Цю залежність можна відобразити у вигляді факторних моделей продуктивності праці і фондовіддачі:
Q/T = Q/N × N/T; Q/F = Q/N × N/F.
Ці залежності відповідають дійсності: продуктивність праці Q/T прямо пропорційна виходу продукції на одиницю предметів праці Q/N і величині предметів праці, що переробляються одним робітником N/T. Аналогічно можна відобразити залежність від даних факторів також фондовіддачі.
Розглянутий приклад переконує у тому, що субфактори для деталізації якісних факторів варто запозичати з якісно однорідних, паралельних моделей одного і того ж об’ємного показника. Причому для практики важливо, щоб паралельно створені моделі містили фактори активного порядку. Мова йде про те, щоб фактори були керовані, тобто щоб шляхом їхнього регулювання в потрібному напрямку можна було досягти бажаної зміни результативних показників.
Керованість факторами – наступний важливий принцип індексного методу. Наприклад, задамося метою сконструювати факторні моделі залежності такого показника, як питома вага господарств (родин), охоплених особистим майновим страхуванням. Чим обумовлюється зміна відсотка охоплення населення цим видом страхування? Очевидно, насамперед, організацією інформаційно-роз’яснювальної роботи серед населення. У свою чергу, остання при інших рівних умовах (вплив засобів масової інформації, рекламних заходів тощо) залежить від того, яку кількість страхових агентів залучено до цієї роботи, і наскільки ефективна їхня діяльність. З огляду на це, можна скласти таку модель факторної залежності показника охоплення населення особистим майновим страхуванням:
x'/x = A/x × x'/A,
де x – загальна кількість господарств (родин) у даному регіоні; x' – кількість господарств (родин), охоплених особистим майновим страхуванням; A – кількість страхових агентів, зайнятих особистим майновим страхуванням.
Відповідно до щойно наведеної моделі, питома вага господарств, охоплених особистим майновим страхуванням, за інших рівних умов зростає прямо пропорційно кількості страхових агентів в розрахунку на 1 тис. господарств A/x, і кількості господарств, застрахованих кожним агентом з цього виду страхування x(/A. Користуючись такими розрахунками, можна визначити вплив даних факторів на показник охоплення населення особистим майновим страхуванням і, головне, використовувати отриману інформацію для активного і цілеспрямованого керування факторами даного процесу.
Можна також побудувати моделі, за допомогою яких не можна впливати на результативний показник. Зокрема відомо, що питома вага застрахованих господарств значною мірою визначається кількістю нещасних випадків, пов’язаних з втратою чи псуванням майна, і поінформованістю населення про такі випадки. Цю залежність можна відобразити формулою:
x'/x = Y/x × x'/Y,
де Y – кількість нещасних випадків, що призвели до втрати чи псування майна населення. Відповідно до даної залежності, питома вага застрахованих господарств зростає прямо пропорційно частці нещасних випадків, пов’язаних із втратою чи псуванням майна B/x, і кількості застрахованих господарств у розрахунку на один нещасний випадок (своєрідний коефіцієнт "сприйняття" нещасних випадків). Така модель містить деяку аналітичну інформацію, але використовувати її як активний механізм поліпшення результативного показника неможливо, оскільки його зміна пов’язана зі свідомою орієнтацією на зростання кількості нещасних випадків Y/x. В даному випадку ми маємо приклад того, як реальні причинно-наслідкові залежності можна підмінити віртуальними або такими, що не мають практичної цінності.
Нами розглянуті порівняно прості варіанти причинно-наслідкових залежностей, у яких якісні показники деталізувались або по горизонталі, або по вертикалі. Проблема деталізації факторних моделей ускладнюється, якщо результативний показник обумовлений і паралельними і послідовними факторами. Це особливий різновид побудови багатофакторних моделей. Суть його полягає в тому, що різні фактори одного і того ж результативного показника повинні бути оцінені за їх економічною значимістю і лише на цій основі певним чином з’єднані у факторну модель. Серед багатьох причин того чи іншого явища з певною умовністю можна виділити причини першого порядку, другого і т.д. Причини одного порядку рівнозначні, але з причинами іншого порядку вони нерівнозначні. Іншими словами, фактори повинні оцінюватися в двох площинах – по вертикалі і по горизонталі. Це дозволяє сформулювати певні умови, дотримання яких необхідне при вирішенні питання щодо послідовності включення факторів у модель.
Оскільки, фактори першого порядку вагоміші, ніж другого, але рівнозначні між собою, вони можуть деталізуватися один за рахунок іншого за схемою зворотного зв’язку. Але фактори другого порядку, будучи рівнозначними, можуть деталізуватись як на зворотній основі, так і за рахунок факторів першого порядку. В той же час вони не можуть деталізуватись за рахунок факторів наступних порядків.
Розглянемо особливості побудови багатофакторних моделей з різними за значимістю факторами на умовному прикладі. Припустимо, потрібно скласти багатофакторну модель залежності обсягу виробництва молока від визначальних його факторів. Виробництво молока безпосередньо зв’язане з такими факторами, як поголів’я корів, наявність кормових ресурсів, виробничих фондів, робочої сили і т.п., складемо ряд двофакторних моделей залежності валових надоїв молока (В) від даних факторів.
| Формула зв’язку | Економічний зміст фактора | |
| кількісного | якісного | |
| В = П × В/П | П – поголів’я корів | В/П – середній надій на одну корову |
| В = К × В/К | К – обсяг використаних кормів (кормоодиниць) | В/К – вихід молока на одну кормову одиницю |
| В = Т × В/Т | Т – чисельність зайнятих у виробництві молока | В/Т – вихід молока в розрахунку на одного працівника |
| В = F × B/F | F – обсяг виробничих фондів молочних ферм | B/F – вихід молока в розрахунку на одиницю вартості виробничих фондів ферм |
| В = Н × В/Н | Н – площа сільсгоспугідь | В/Н – виробництво молока на одиницю сільгоспугідь |
| В = Т' × В/Т' | Т' – чисельність доярок | В/Т' – виробництво молока в розрахунку на одну доярку |
| В = F' × B/F' | F' – активна частина виробничих фондів ферм | B/F' – вихід молока на одиницю вартості активної частини виробничих фондів ферм |
Приведені кількісні фактори валового надою молока і похідні від них якісні фактори, виходячи з їхньої значимості, можна розподілити на декілька рівнів. До найбільш активних, які безпосередньо впливають на результативний показник відносяться фактори перших двох моделей – поголів’я корів і наявність кормів. Вони є першоосновою утворення результативного показника (фактори продукуючого характеру) і мають певну ступінь взаємозаміни. Тому є всі підстави віднести їх до факторів першого порядку. У відношенні до результативного показника вони рівноцінні, тому що один фактор без іншого не уявляється.
Дві наступні моделі містять фактори "обслуговуючого" характеру (робоча сила і виробничі фонди), які також характеризуються певною взаємозаміною. Вони менш істотні порівняно з першими, тому що при відсутності перших їх неможливо задіяти. Разом з тим вони рівноцінні по відношенню до результативного показника.
Нарешті, останній фактор – площа сільськогосподарських угідь хоч і має пряме відношення до виробництва молока, але його зв’язок з результатом певним чином опосередкований і значно слабкіший, ніж у попередніх факторів. Тому він займає третє місце в причинно-наслідкових зв’язках.
Подібний аналіз ієрархічного розподілу факторів дозволяє на визначеному етапі обмежити кількість залучених до аналізу факторів і, найголовніше, упорядкувати процес складання багатофакторних моделей.
Так, відносні фактори першого порядку – середній надій на корову В/П і середній вихід молока на одиницю корму В/К можуть деталізуватися тільки за схемою зворотного зв’язку, тобто:
В/П = В/К × К/П;
В/К = В/П × П/К.
Дійсно, середній надій на корову В/П залежить від рівня годівлі худоби К/П та "віддачі" одиниці корму В/К, з іншого боку, "віддача" одиниці корму В/К залежить від продуктивності тварин В/П і кількості голів, що приходяться на одиницю корму (П/К у даному пипадку є своєрідним показником якості кормів, тому що чим більшу кількість худоби можна нагодувати одиницею корму, тим він якісніший).
Отже, в межах розгляду факторів першого порядку одержимо дві можливі моделі індексного аналізу виробництва молока:
В = П × В/П = П × В/К × К/П;
В = К × В/К = К × В/П × П/К.
Діючи аналогічним чином у межах взаємодії факторів другого порядку та деталізуючи їх за рахунок факторів першого порядку, можна створити велику серію моделей багатофакторного аналізу виробництва молока. Наприклад, якщо в якості вихідної взяти модель В = Т × В/Т, то її деталізований вигляд може мати такий різновид моделей:
В = Т × В/К × К/П × П/F' × F'/F × F/T' × T'/T;
В = Т × В/П × П/К × К/F' × F'/F × F/T' × T'/T;
В = Т × В/П × П/К × К/Т' × Т'/F' × F'/F × F/T;
B = T × B/K × K/T' × T'/П × П/F' × F'/F × F/T.
Незважаючи на деякі розбіжності, сутність усіх цих моделей залишається незмінною, оскільки заміна прямих факторів зворотними чи деякою їхньою перестановкою суті питання в принципі не змінює. Істотне значення має той факт, що кожна з них тим чи іншим способом охоплює всі обрані нами фактори і не суперечить логіці розвитку подій (при перевірці реальності зв’язку результативного показника з факторами зручніше аналізувати логічність розгортання факторів праворуч-ліворуч). Тому для практичних цілей досить використовувати одну з наведених моделей.
У нашому прикладі є фактор третього порядку – площа сільськогосподарських угідь Y. Його також можна деталізувати за рахунок факторів першого і другого порядків і тим самим поглибити факторну модель. Але якщо проаналізувати математично можливі варіанти "стикування" даного фактора з попередніми, з’ясовується, що жоден з цих варіантів не має економічного змісту. Це означає, що для включення фактора сільськогосподарських угідь у даний ланцюг причинно-наслідкових залежностей потрібно введення в коло факторів певного сполучного елемента. Що стосується зв’язку показників площі сільськогосподарських угідь і поголів’я корів, то на цій основі можна побудувати двофакторну модель типу:
В/Н = В/П × П/Н.
Тут зв’язок економічно змістовний: виробництво молока на одиницю площі сільськогосподарських угідь В/Н залежить від продуктивності корів В/П та насиченості поголів’я на одиницю сільськогосподарських угідь П/Н. Доповнивши дану модель іншими родинними факторами, можна перейти до розгортання іншої зрізу причинно-наслідкових зв’язків і до створення багатофакторних моделей в іншому напрямку.
Наприклад, додатково уведемо фактор Н( – площу кормових культур. У зв’язку з цим модель матиме такий вигляд:
В/Н = В/П × П/К × К/Н' × Н'/Н.
Фактори, що з’явилися (К/Н' – врожайність кормових культур і Н'/Н – питома вага площі кормових культур у загальній площі сільгоспугідь) безпосередньо впливають на виробництво молока. Можливі серії багатофакторних моделей з урахуванням цих обставин залишаємо на роздуми читача.
Загальний індекс зміни валового надою молока звітного періоду порівняно з базовим визначається формулою:
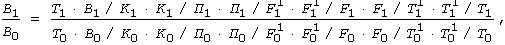
де Т – чисельність працівників, зайнятих у виробництві молока; В/К – вихід молока на кормову одиницю (показник якості кормів); К/П – рівень годівлі корів; П/F' – кількість корів, що приходиться на одиницю вартості активної частини виробничих фондів; F'/F – питома вага активної частини виробничих фондів у їх загальній вартості; F/T( – фондоозброєність в розрахунку на одну доярку; Т'/Т – питома вага кількості доярок у загальній кількості працівників, зайнятих у виробництві молока.
Далі загальний індекс (в даному випадку індекс валового надою молока) розкладається на індекси його факторів за правилом – фактор, що індексується, який по чисельнику і знаменнику береться на рівні відповідно звітного і базового періоду, а всі інші фактори – на рівні одного і того ж періоду. Наприклад, індекс чисельності працівників, зайнятих у виробництві молока (Т), вираховується за формулою:
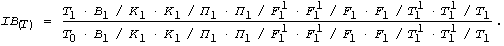
І останнє зауваження. Факторний аналіз будь-якого явища слугує лише вихідною інформацією для подальшого аналітичного дослідження проблематики, пов’язаної з негативним впливом того чи іншого фактора на результативний показник. Скажімо, у нашому прикладі виявиться, що найбільший негативний вплив на валове виробництво молока має від’ємний фактор К/П (рівень годівлі корів). Причини зменшення рівня годівлі мають бути проаналізовані в усіх аспектах, пов’язаних з цим явищем – станом виробництва кормів, їх якістю, технологією приготування, згодовування, збереження, тощо. Лише при такій умові багатофакторний індексний аналіз може в повній мірі реалізувати свою практичну цінність. А це в свою чергу вимагає від дослідника професійного володіння всією конкретикою досліджуваного явища.
Опубліковано : Андрієнко В.Ю. Cтатистичні індекси в економічних дослідженнях. – К. : 2004 р., с. 92 – 106.
