Миля Герберштейна
Жарких М.І.
Термінологія мір віддалі у Герберштейна
Класифікація віддалей Герберштейна
Застосування методів математичної статистики для обробки повідомлень історичних джерел здатне збагатити наше уявлення про минуле і видобути нову інформацію з документів, давно введених у науковий обіг. В даній статті я спробую проілюструвати цю тезу на прикладі з історичної метрології.
Австрійський барон Сигізмунд Герберштейн (1486-1566 рр.) – автор славнозвісних "Записок про московські справи" [1] – склав досить докладний географічний опис Східної Європи. Цей опис охоплює землі Великого князівства Литовського (Литву, Білорусію та частково Україну), землі Московської держави, території татарських держав. Він складений за принципом путівника, в якому зазначаються назви географічних об’єктів, віддаль від попереднього пункту опису, подекуди – напрямок шляху або розміри описуваного об’єкту. Майже всі віддалі в описі Герберштейн подає в милях, тому важливо з’ясувати, яка величина цієї міри і наскільки точними є орографічні дані Герберштейна.
Термінологія мір віддалі у Герберштейна
Для визначення віддалі Герберштейн використовує різні терміни: італійська миля, верста, день шляху, екзотична татарська міра "чункас" (на його думку, 5 верст). Але всі ці міри є епізодичними, а основними термінами є "миля" та "німецька миля".
Неважко переконатись, що просто "миля" тотожня "німецькій милі", але не "італійській милі". Ця остання згадується Герберштейном лише 4 рази:
1) пояснюючи, що таке "верста", він прирівнює її до італійської милі (с. 129);
2) зазначаючи довжину Азовського моря – 300 італійських миль (с. 181);
3) зазначаючи ширину Керченської протоки – 2 італійських милі (с. 182; можна припустити, що в цих двох випадках був використаний якийсь опис Чорного моря італійського походження);
4) вказуючи, що польсько-литовський кордон йде по річці Ясонка в одній італійській милі від Парчева (с. 254).
З цього можна виснувати, що Герберштейн вживає термін "італійська миля" для точного означення невеликої віддалі, яка у звичних для нього німецьких милях була б маленьким дробним числом (а дробних чисел він не любить і майже не вживає, як побачимо далі).
Московська міра віддалі "верста" у Герберштейна зустрічається частіше, але переважна частина віддалей, узятих з московських джерел, подана в милях. Для цього Герберштейну довелося виконати досить складну роботу по переведенню даних своїх інформаторів у звичні для Західної Європи милі.
Класифікація віддалей Герберштейна
Шлях Герберштейна по Європі пролягав через країни з різною культурною орієнтацією. Я розділив всі ділянки його шляху на 4 групи:
1) "Німеччиною" в контексті даної роботи я називаю власне німецькі князівства та країни, пов’язані з ними тісними культурними та політичними зв’язками (Угорщина, Чехія, Силезія);
2) "Польщею" в контексті даної роботи я називаю землі історичної Польщі початку 16 ст.;
3) "Литвою" в контексті даної роботи я називаю землі Великого князівства Литовського згідно з кордонами початку 16 ст.;
4) "Московією" в контексті даної роботи я називаю землі Великого князівства Московського згідно кордонів початку 16 ст.
Для ділянок 1-ї та 2-ї груп Герберштейн подає тільки запис ділянок власного шляху; для 3-ї та 4-ї груп дано віддалі як для тих ділянок, якими проїздив посол, так і для тих, якими він не проїздив, але які потрібні йому для опису місцевості. Розрізнення "ділянок шляху", де Герберштейн міг спиратися на власні враження і самостійно оцінювати віддалі, та "ділянок опису", де він мусив використовувати відомості інших людей, виявилося істотним. Для груп ділянок 1-3 миля була звичної мірою віддалі, тому тут Герберштейн міг звіряти свої спостереження з даними місцевих жителів; у Московії милі не використовувались, і тут всі визначення віддалей в милях є особистою заслугою Герберштейна.
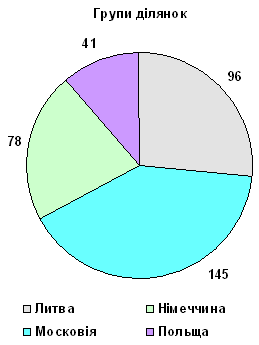
Малюнок 1. Число ділянок шляху по групах.
Для статистичного аналізу було складено невелику базу даних, до якої вносилися назва ділянки, її протяжність в милях (враховувалися також наявні у Герберштейна варіанти віддалі). Далі ці віддалі вимірювалися за сучасними картами [2].
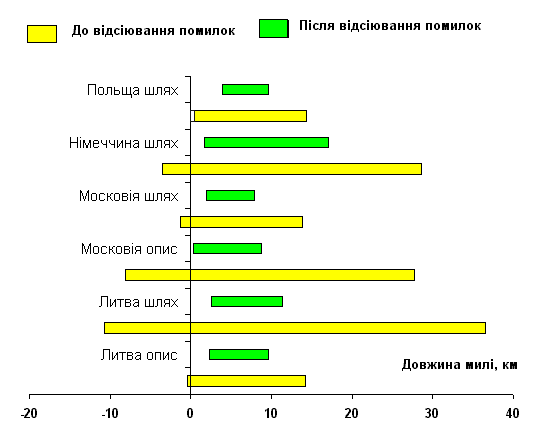
Перш ніж аналізувати нагромаджені дані, довелося виконати фільтрацію явно помилкових спостережень. Для цього застосовано правило "трьох стандартних відхилень". Для кожної групи ділянок (там де треба – окремо для опису та для шляху) вираховувалося стандартне відхилення σ:
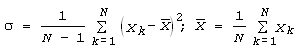
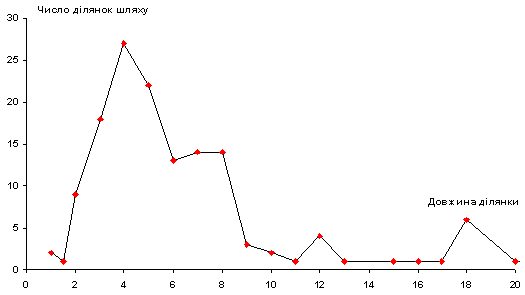
оскільки ця величина обчислювалася з урахуванням усіх значень (в тому числі й помилкових – таких, що різко виділяються серед загалу), то вона є порівняно великою. Далі кожне окреме значення Xk перевірялося на належність до довірчого інтервалу за правилом:
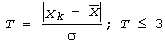
В результаті такої перевірки ми одержуємо групу значень, які належать до генеральної сукупності (відхилення не перевищує 2σ), та групу значень, підозрілих на різке виділення (відхилення 2σ..3σ). Кожне з підозрілих значень вилучалося з набору даних, заново обчислювалося стандартне відхилення (через вилучення підозрілого елементу воно зменшувалось); підозріле значення заново перевірялося на належність до довірчого інтервалу з цим зменшеним значенням відхилення. В разі виходу значення за межі довірчого інтервалу значення помічалося як помилкове і вилучалося з подальших розрахунків.
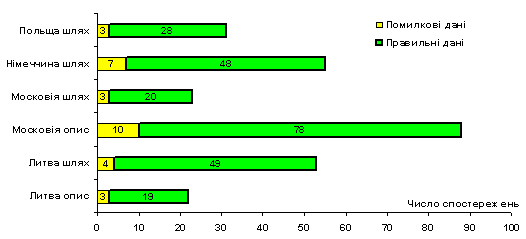
Малюнок 2. Розподіл числа помилок по ділянках.
Дана процедура застосовувалась до тих пір, поки лишались кандидати на вилучення. Всього з 272 ділянок помилковими виявилися 30, правильними (тобто такими, які не виділяються різко з сукупності собі подібних) – 242. Розподіл їх зображено на малюнку 2.
В наступній таблиці показано кілька прикладів помилок. Скажімо, в Литві від Гродно до Перлої Герберштейн занотував лише 2 милі, тоді як між ними – 74 кілометри, що на 29 стандартних відхилень перевищує середнє значення для даної групи ділянок (гадаю, що тут мало бути 12 миль, але Герберштейн десь припустився помилки). Тому це спостереження було відкинуто.
Таблиця 1. Кілька прикладів найяскравіших помилок.
| Група ділянок | Назва ділянки | Віддаль в милях | Сучасна віддаль в км | Найбільша миля, км | Сторінки | 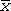 |
σ | T |
| Литва шлях | Гродно-Перлоя | 2 | 74 | 49.3 | 233 | 7.00 | 1.47 | 28.77 |
| Московія опис | Новгород-устя р.Волхов | 6 | 192 | 34.9 | 150 | 4.51 | 1.40 | 21.74 |
| Московія опис | Пермь-устя р.Вішера | 10 | 204 | 21.5 | 162 | 4.51 | 1.40 | 12.13 |
| Польща шлях | Олешно-Кшепице Стар. | 2 | 25.5 | 17 | 254 | 6.77 | 0.96 | 10.65 |
Малюнок 3 ілюструє значення процедури вилучення помилкових спостережень для подальшої роботи. Перший набір даних показує характеристики вибірок без відкидання помилкових даних (в інтервалі між лівим і правим кінцем стрічки зосереджено 99.7 % всіх спостережень, що відповідає межам 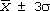 ); як бачимо, внаслідок присутності помилкових спостережень розбіжності дуже великі, починаються мало не від нуля, або навіть з негативних значень. Другий набір даних змальовує аналогічні інтервали після відсіювання: середні значення зменшились (це пов’язано з тим, що всі помилки дають занижені віддалі в милях, тобто завищені значення для довжини милі); але набагато істотніше знизилися стандартні відхилення.
); як бачимо, внаслідок присутності помилкових спостережень розбіжності дуже великі, починаються мало не від нуля, або навіть з негативних значень. Другий набір даних змальовує аналогічні інтервали після відсіювання: середні значення зменшились (це пов’язано з тим, що всі помилки дають занижені віддалі в милях, тобто завищені значення для довжини милі); але набагато істотніше знизилися стандартні відхилення.
Малюнок 3. 99.7-% довірчі інтервали для довжини милі.
Найбільшу користь для визначення довжини милі несуть ділянки шляху, а не опису. Вивчення їх показує дві істотні для подальших розрахунків особливості:
- Герберштейн майже скрізь визначає свої віддалі цілими числами (малюнок 4). Тілки в одному (!) випадку він зазначає віддаль в півтори милі;
- переважна більшість ділянок шляху має невелику довжину – до 8 миль (натомість в описі часто зустрічаються дуже великі віддалі: якщо середня ділянка шляху дорівнює 7 милям, то середня ділянка опису – 52 милям).
Малюнок 4. Розподіл ділянок шляху за довжиною.
Оскільки об’єктивно дробні числа все ж таки зустрічаються (попри всю нелюбов Герберштейна до них), то нема підстав сподіватись, що заокруглені ним до цілих значень віддалі будуть точно відповідати еталонові. Тому миля Герберштейна – це не точка на числовій осі, а інтервал значень, межі якого розраховуються у наступний спосіб.
Позначимо довжину ділянки k в милях через Mk; позначимо Mk min = Mk – 0.5; Mk max = Mk + 0.5; в силу зауваженої вище дискретності будь-яка віддаль, що лежить між Mk min та Mk max позначається в нашому джерелі як Mk.
Позначимо довжину ділянки k в кілометрах через Lk; тепер із співставлення цих довжин ми можемо вирахувати мінімальну та максимальну довжину милі за формулами:
Xk min = Lk / Mk max; Xk max = Lk / Mk min;
Якщо наші міркування вірні, то функції розподілу величин Xk min та Xk max повинні мати суттєво різні середні значення.
За допомогою дисперсійного аналізу ми можемо підтвердити або спростувати припущення про істотність різниці між мінімальною та максимальною довжиною милі.
Нагадаю, що дисперсійний аналіз покликаний порівнювати середні значення величини відгуку в групах спостережень, які різняться між собою величиною незалежної змінної (предиктора). В даному випадку відгуком є довжина милі, предиктором – належність даного виміру до групи "мінімальна довжина" чи "максимальна довжина". Аналіз виконувався окремо для всіх ділянок шляху та всіх ділянок опису.
Таблиця 2. Дисперсійний аналіз відмінності між мінімальною та максимальною довжиною милі.
| Група ділянок | Джерело дисперсії | Сума квадратів | Число ступенів свободи | Середній квадрат | Значення критерію Фішера | Імовірність |
| Шлях | Предиктор | 175.4 | 1 | 175.4 | 47.0 | 4.2E-11 |
| Шлях | Залишок | 1073.9 | 288 | 3.7 | ||
| Шлях | Разом | 1249.3 | 289 | 4.3 | ||
| Опис | Предиктор | 3.61 | 1 | 3.61 | 1.81 | 0.18 |
| Опис | Залишок | 382.2 | 192 | 1.99 | ||
| Опис | Разом | 385.8 | 193 | 1.99 |
Як видно з таблиці 2, значення предиктора (тобто факт належності значення до мінімальних чи максимальних довжин) є дуже істотним для шляху (в останньому стовпчику "імовірність" означає імовірність гіпотези, що значення предиктора неістотне для відгуку; мізерне значення імовірності означає істотність впливу предиктора). Натомість для групи ділянок опису значення предиктора не є важливим.
Висновок з даного етапу дисперсійного аналізу такий: дискретність значень довжини ділянок в милях є істотною для шляху і неістотною для опису.
Наступною гіпотезою, яку треба перевірити за допомогою дисперсійного аналізу, є вплив країни, до якої належить ділянка шляху, на довжину милі.
Таблиця 3. Дисперсійний аналіз впливу країни на максимальну довжину милі.
| Група ділянок | Джерело дисперсії | Сума квадратів | Число ступенів свободи | Середній квадрат | Значення критерію Фішера | Імовірність |
| Шлях | Предиктор | 316.1 | 3 | 105.4 | 32.5 | 4.8E-16 |
| Шлях | Залишок | 456.5 | 141 | 3.2 | ||
| Шлях | Разом | 772.7 | 144 | 5.4 | ||
| Опис | Предиктор | 31.7 | 1 | 31.7 | 16.95 | 8.2E-05 |
| Опис | Залишок | 177.8 | 95 | 1.87 | ||
| Опис | Разом | 209.5 | 96 | 2.18 |
Таблиця 4. Дисперсійний аналіз впливу країни на мінімальну довжину милі.
| Група ділянок | Джерело дисперсії | Сума квадратів | Число ступенів свободи | Середній квадрат | Значення критерію Фішера | Імовірність |
| Шлях | Предиктор | 104.6 | 3 | 34.9 | 25.0 | 4.9E-13 |
| Шлях | Залишок | 196.6 | 141 | 1.39 | ||
| Шлях | Разом | 301.3 | 144 | 2.09 | ||
| Опис | Предиктор | 32.8 | 1 | 32.8 | 22.3 | 8.2E-06 |
| Опис | Залишок | 139.9 | 95 | 1.47 | ||
| Опис | Разом | 172.7 | 96 | 1.80 |
Ділянки групи "шлях" ми розділили на 4 країни; ділянки групи "опис" присутні тільки для двох з цих країн. Як видно з результатів дисперсійного аналізу, предиктор "країна" в усіх випадках є істотним, тому середнє значення довжини милі Герберштейна залежить від того, по якій країні він проїжджав.
Графічне представлення інтервалів довжин, які відповідають поняттю "миля Герберштейна" (малюнок 5) дозволяє стверджувати, що різниця між Польщею та Литвою не є значною; натомість різниця між Німеччиною (миля 7..9.3 км) – Польщею-Литвою (миля 5.5..7 км) – Московією (миля 4.4..4.9 км) досить виразна. Довжина милі зменшується в міру того, як погіршуються дороги.
Сам Герберштейн двічі вказує, що він числить в милі 5 верст [3], що відповідає нашим розрахункам.
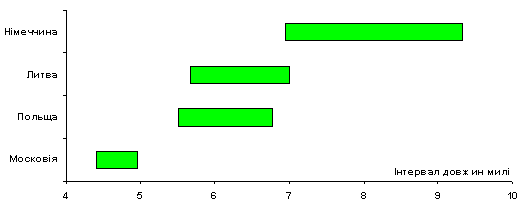
Малюнок 5. Довжина милі Герберштейна залежить від країни.
Нарешті, для тих країн, де представлені як опис, так і шлях, треба порівняти значення милі по цих групах (тобто предиктором виступатиме належність ділянки до опису чи шляху).
Таблиця 5. Дисперсійний аналіз впливу опису/шляху на максимальну довжину милі.
| Група ділянок | Джерело дисперсії | Сума квадратів | Число ступенів свободи | Середній квадрат | Значення критерію Фішера | Імовірність |
| Литва | Предиктор | 15.3 | 1 | 15.3 | 7.70 | 7.2E-03 |
| Литва | Залишок | 131.1 | 66 | 1.99 | ||
| Литва | Разом | 146.4 | 67 | 2.19 | ||
| Московія | Предиктор | 3.13 | 1 | 3.13 | 1.77 | 0.19 |
| Московія | Залишок | 169.6 | 96 | 1.77 | ||
| Московія | Разом | 172.7 | 97 | 1.78 |
Таблиця 6. Дисперсійний аналіз впливу опису/шляху на мінімальну довжину милі.
| Група ділянок | Джерело дисперсії | Сума квадратів | Число ступенів свободи | Середній квадрат | Значення критерію Фішера | Імовірність |
| Литва | Предиктор | 1.36E-02 | 1 | 1.36E-02 | 1.68E-02 | 0.90 |
| Литва | Залишок | 53.7 | 66 | 0.81 | ||
| Литва | Разом | 53.7 | 67 | 0.80 | ||
| Московія | Предиктор | 0.55 | 1 | 0.55 | 0.39 | 0.53 |
| Московія | Залишок | 132.9 | 96 | 1.38 | ||
| Московія | Разом | 133.5 | 97 | 1.38 |
З аналізу випливає, що тільки в одному випадку (максимальна довжина милі в Литві) різниця між описом та шляхом істотно впливає на довжину милі. В цілому ж цей фактор треба визнати неістотним.
Проведений аналіз дозволяє зробити певні припущення щодо методики розрахунку віддалей в орографії Герберштейна.
По-перше, істотна залежність довжини милі від країни, якою проїздив мандрівник (власне, від якості доріг в тій чи іншій країні) наводить на думку, що за основу розрахунку брався час проїзду. Зменшення швидкості руху внаслідок погіршення доріг (в Московії особливо наприкрилися часті переправи через малі річки) дуже тяжко оцінити об’єктивно – ми бачимо, що Герберштейну це не вдалося.
По-друге, істотне значення має дискретність віддалей, згаданих Герберштейном, що відбивається в інтервалах довжини милі.
По-третє, неістотна різниця між довжиною милі, обрахованої за описом і шляхом, свідчить про те, що Герберштейн на підставі власних спостережень вирахував довжину московської версти у звичних для нього милях і за допомогою цього модуля перевів віддалі у верстах на віддалі в милях. Питання про те, якою одиницею довжини користувалися його інформатори по Литві, лишається відкритим.
Слід зауважити, що двократне зменшення "милі для Московії" в порівнянні з "милею для Німеччини", яке нам може видатись дуже серйозним недоліком, було далеко не катастрофічним для сучасників Герберштейна. Адже для них відомості його путівника мали не лише теоретичне орографічне значення, але й цілком практичне: за який час можна проїхати з пункту А в пункт В [4] ? А для відповіді на це питання змінна миля Герберштейна підходила як найкраще.
1. Герберштейн С. Записки о Московии. – М.: 1988. Далі я скрізь посилатимусь на це критичне видання. Повний текст записок С.Герберштейна нині доступний у вебі на сайті "".
2. Для країн Європи я використав карти з "Атласа мира" (М.: 1967) в масштабі 1:1500000, на яких позначена переважна більшість навіть дрібних містечок, згаданих Герберштейном; територія СРСР в цьому атласі подана тільки в масштабі 1:3000000, внаслідок чого багатьох потрібних пунктів нема, тому доводилось використовувати адміністративні карти областей масштабу 1:400000.
3. Герберштейн С., с. 123: від Новгорода до Москви 600 верст, або 120 миль; с. 202: шлях в 1700 верст, або 340 миль.
4. Так і таджицька міра: "чакрим був мірою не довжини, а зусиль, котрі людина мусить витратити, щоб досягнути мети" (Гумилёв Л.Н. Открытие Хазарии.- М., 1966.- С. 19).
Стаття закінчена 1.07.1996 р.
Вперше опублікована: Жарких М.І. Миля Герберштейна. – Археометрія та охорона історико-культурної спадщини, 1998 р., т. 2, с. 32 – 37.
