4.3. Стратегія оптимального розподілення наявних кредитних ресурсів банку серед запропонованих бізнес-проектів
Брітченко І.Г.
Наявність пріорітетного ряду, побудованого на порівнянні коефі-цієнтів ефективності інвестиційних проектів, не вирішує усіх питань, які виникають перед банком. Залишається невирішеною проблема оптимального розподілення наявних у комерційного банку ресурсів за усіма запропонованими інвестиційними проектами, хоча подальшому аналізу та розгляду належать лише ті інвестиційні проекти, коефіцієнти ефективності яких більші одиниці. При вирішенні даної проблеми повинні враховуватися наступні обставини:
– ресурси комерційного банку, як і будь-якого іншого інвестора, обмежені об’єктивними можливостями;
– клієнт, що запитує конкретну суму кредиту, не завжди погодиться з меншою сумою, запропонованою йому банком;
– строки, передбачені інвестиційними проектами, можуть дуже відрізнятися один від одного та від строків, на які банк згодний надати інвестиційні ресурси;
– інвестиційні ресурси банку повинні бути максимально задіяні, тобто повинна зводитися до мінімуму невитребуваність ресурсів одночасно з максимальною ефективністю усіх інвестуємих коштів (відповідно з наявним пріоритетним рядом);
– у випадку, якщо неможливо задовольнити вимоги усіх наявних клієнтів через обмеженість ресурсів банку, необхідно задовольняти потреби найбільш економічно вигідних клієнтів, тобто тих клієнтів, інвестування яких надасть банку найбільший економічний ефект.
Дана задача має математичну модель, для складання якої уведемо наступні позначення з урахуванням викладеного вище.
Позначення:
n – кількість інвестиційних проектів;
i – i-й інвестиційний проект;
Аі – сума кредиту, необхідна для здійснення i-го інвестиційного проекту;
Ві – строк здійснення і-го інвестиційного проекту;
N – загальна сума усіх коштів, яку може виділити інвестор на здійснення усіх проектів;
Рі – узагальнюючий коефіцієнт ефективності і-го інвестиційного проекту.
Невизначеними величинами даної задачі є:
Xі – сума коштів, яка може бути інвестована в і-ий інвестиційний проект (при максимальній корисності для інвестора);
Yі – строк, на який банку вигідно надавати інвестиційні ресурси під і-ий інвестиційний проект.
Обмеженнями даної задачі є:
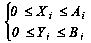
Дана задача має математичну модель, яка є функцією мети, що прагне до максимального значення.
Функція мети виглядає наступним чином:
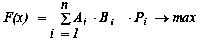 |
(4.16) |
Функція мети представляє суму всіх інвестуємих банком коштів у певний інвестиційний проект за визначений проміжок часу з урахуванням ефективності інвестиційних проектів. Тобто, якщо інвестиції за визначений проміжок часу будуть найбільш ефективними, то вони будуть такими і у будь-який час.
Поставлена задача має модель, описану вище та вирішується за допомогою почергового пошуку оптимальних значень або шляхом простого перебору різних варіантів інвестування. Вирішення такого роду задач без використання ЕОМ практично неможливе, тому що для цього необхідно власноруч прораховувати величезну кількість можливих варіантів розподілення інвестиційних ресурсів. Разом з тим, програмне забезпечення для вирішення даної задачі не відноситься до розряду складних, цінних і наукомістких програмних продуктів. Це дозволяє зробити використання запропонованої методики широко росповсюдженою та досяжною кожному інвестору, який володіє комп’ютером будь-якої модифікації.
Описана задача грунтується на програмі, виконаній на мові програмування «Turbo-Pascal-7.0». Для її вирішення необхідно:
1. Увести кількість наявних інвестиційних проектів.
2. Увести максимальний розмір наявних у інвестора ресурсів.
3. Увести дані кожного інвестиційного проекту (запрошувана сума, строк, узагальнений коефіцієнт ефективності проекту).
4. Отримати оптимальні значення розподілення інвестиційних ресурсів.
Програма дозволяє отримати максимальне значення заданої функції та спостерігати її зміну при різних параметрах інвестиційних проектів, корегувати ці параметри у разі необхідності.
Програма та математична модель дозволяє вирішувати й інші задачі, вона дозволяє спостерігати вплив різної величини або обмеження на оптимальний розподіл інвестиційних ресурсів. Найбільш типовими є зміни величини «N», тобто інвестиційних можливостей банку, яка після закінчення визначеного проміжку часу повинна збільшитися. Це повинно відбутися тому, що частина отриманої від ефективного розподілення ресурсів прибутку буде направлятися банком на збільшення інвестиційних фондів. Такий приріст банківського капіталу можливий тільки за умови ефективного інвестування наявного. Математична модель допомагає прогнозувати строки та розмір приросту банківського капіталу, однак повне прогнозування цих процесів затруднене рядом зовнішніх факторів, що знаходяться за межами внутрішньої банківської політики. До таких факторів можна віднести зміни в податковому законодавстві, зміни цін на ресурси, що складають собівартість банківського продукту (наприклад, зміни на ринку трудових ресурсів) та ін.
Запланувати та спрогнозувати різні події, що впливають на інвестиційні процеси, використовуючи зазначену модель, неможливо, тому що в економіці не існує зовсім чистих явищ, що повністю відповідають будь-яким моделям і схемам. Запропонована модель не враховує, наприклад, такого чинника, як особисті стосунки між керівниками підприємтсв, включаючи і керівника банку, ряд раптових подій та ін. Разом з тим модель дозволяє прослідкувати вплив такого макроекономічного фактора як інфляція на інвестиційну привабливість проектів і розподілення інвестиційних ресурсів; дозволяє бачити взаємозв’язок і взаємний вплив на розподілення інвестиційних ресурсів забезпеченості інвестицій та індивідуальних характеристик виконавця інвестиційного проекту.
Для запропонованої методики оптимального розподілення інвестиційних ресурсів властивий той факт, що за допомогою зазначених методів можна визначити оптимальність розподілення ресурсів на конкретний момент часу та за наявності певних інвестиційних проектів (табл. 4.6). Однак після закінчення деякого часу до банку можуть звернутися інші клієнти з новими інвестиційними проектами або, у результаті змін економічних умов, інвестиційні проекти, що пропонувалися раніше, стануть більш ефективними та економічно вигідними. У такому випадку інвестору доведеться вирішувати аналогічну задачу, але вже на інший момент часу та з іншими характеристиками. У випадку необхідності можна нову задачу доповнити і даними про проінвестовані (діючі) проекти для наглядного порівняння та економічного аналізу. Такий прийом може знадобитися при достроковому поверненні інвестованих коштів позичальником або наявності дострокового відкликання ресурсів інвестором.
Дана методика може використовуватися практично за будь-якої кількості інвестиційних проектів і будь-яких економічних характерристик. Вона прийнятлива як для невеликих, так і для великих банків та їх об’єднань.
Розглянемо практичні аспекти використання методики. Припустимо, що до банку звернулося одинадцять підприємств, тобто є одинадцять інвестиційних проектів. Характеристики наявних проектів відображені у табл. 4.7.
Крім зазначених характеристик інвестиційних проектів відомі наступні дані: прогнозований річний відсоток інфляції (Пінф.) складає 16 %; відсоток, що сплачується при купівлі ресурсів (П2) складає 20 %; річний відсоток, що сплачується банком по залишках на рахунках клієнтів (П3) складає 4 %. Крім того, що інвестиційні можливості (М ) складають 600 000 грн.
Таблиця 4.6 Характеристика інвестиційних проектів банку
| i-ий інвестиційний проект / Параметри інвестиційного проекту | Од. виміру | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Сума кредиту, необхідна для здійснення проекту (Аi ) | тис. грн | 50 | 100 | 120 | 80 | 150 | 40 | 60 | 70 | 110 | 90 | 100 |
| Строк здійснення інвестиційного проекту (Вi) | сут. | 90 | 60 | 30 | 60 | 120 | 90 | 50 | 40 | 80 | 90 | 70 |
| Середньомісячний сукупний прибуток від інших послуг, наданих клієнту (П) | грн | 800 | 1 100 | 1200 | 1 000 | 900 | 400 | 800 | 900 | 110 | 900 | 1 000 |
| Розмір середньомісячних залишків на рахунку (Оск ) | грн | 3 000 | 1 500 | 7 000 | 6 000 | 2 000 | 1 000 | 4 000 | 5 000 | 4 000 | 6 000 | 3 000 |
| Річна відсоткова ставка, яку згодний платити клієнт за надані ресурси (П1 ) | % | 38 | 43 | 41 | 46 | 44 | 50 | 44 | 46 | 45 | 40 | 41 |
| Коефіцієнт, який враховує забезпеченість проекту (Коб ) | 0,8 | 0,8 | 1 | 0,7 | 0,9 | 0,5 | 0,9 | 1 | 0,9 | 0,8 | 0,7 | |
| Індивідуальний коефіцієнт, який враховує перспективність (Кп) | 1 | 0,9 | 0,7 | 0,9 | 0,8 | 0,7 | 1 | 0,8 | 0,7 | 0,9 | 1 | |
| Коефіцієнт ефективності проекту (Ке) (Рі) | 1,349 | 1,042 | 1,090 | 1,148 | 1,038 | 0,618 | 1,600 | 1,463 | 1,034 | 1,109 | 1,062 |
Для вирішення такої задачі необхідно визначити коефіцієнти ефективності кожного інвестиційного проекту. Використовуючи запропоновану методику, нескладно підрахувати, що коефіцієнт ефективності першого інвестиційного проекту (Ке1) складає:
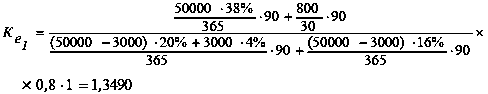
Аналогічно можна визначити коефіцієнти ефективності інших інвестиційних проектів, які будуть складати:
Ке1 = 1,349; Ке2 = 1,042; Ке3 = 1,090;
Ке4 = 1,148; Ке5 = 1,038; Ке6 = 0,618;
Ке7 = 1,600; Ке8 = 1,463; Ке9 = 1,034;
Ке10 = 1,109; Ке11 = 1,062.
Пріорітетний ряд виглядає наступним чином:
Р6, Р9, Р5, Р2, Р11, Р3, Р10, Р4, Р1, Р8, Р7 → max
При подальших розрахунках інвестиційний проект під номером 6 не буде прийматися у розрахунок, оскільки його коефіцієнт ефективності (Ке) менше 1.
Значення коефіцієнтів ефективності кожного інвестиційного проекту також занесені до табл. 4.6.
Підставивши дані, що маємо, до запропонованої програми, отримаємо рішення задачі у вигляді табл. 4.7.
Таблиця 4.7. Дані рішення задачі
| i-ий інвестиційний проект / Параметри інвестиційного проекту | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Сума інвестуємих коштів | 50 000 | 0 | 0 | 40 000 | 150 000 | 60 000 | 0 | 110 000 | 90 000 | 100 000 |
| Оптимальний строк інвестування | 90 | 0 | 0 | 60 | 120 | 50 | 0 | 80 | 90 | 70 |
Табл. 4.7 представляє собою оптимальне розподілення наявних у банку інвестиційних ресурсів у розмірі 600 грн серед запропонованих одинадцяти інвестиційних проектів.
При цьому проекти під номерами 2; 3; 6; 8 інвестуватися не повинні.
Інвестиційні проети під номерами 1; 4; 5; 7; 9; 10; 11 будуть інвестуватися у розмірах та на строк, вказаний у таблиці.
У випадку, якщо один з клієнтів відмовиться від інвестиційного проекту, то задача буде вирішена з новими умовами та наявні інвестиційні ресурси будуть розподілені з урахуванням параметрів, що змінилися.
Основні терміни і поняття
Регіональна стратегія банку, оптимальна кількість філій у регіоні, достатня кількість філій у регіоні, експертна оцінка, оптимальний розподіл філій серед регіонів, ресурсонадлишковість і ресурсонедостатність, бізнес-проект, кредитні ресурси, кредитний ризик, банківська стратегія зниження кредитного ризику, платоспроможність, активи банку, ліквідність банківських активів, забезпечення кредиту, застава, заклад, оцінка майна, стратегія оптимального розподілення кредитних ресурсів, пріоритетний ряд інвестиційного проекту.
Запитання для самоконтролю
Що таке регіональна стратегія комерційного банку?
Як розрахувати оптимальну та достатню кількість банківських філій у регіоні?
Розкрийте вплив експертної оцінки на регіональну стратегію комерційного банку.
У чому основна ідея стратегії оптимального розподілу банкіських філій серед регіонів України?
У чому полягає банківська стратегія зниження кредитного ризику?
Як платоспроможність клієнта впливає на забезпеченість кредитних ресурсів банку?
Розкрийте роль застави у процесах банківського кредитування.
Які методи оцінки заставного майна Вам відомі?
У чому полягає стратегія оптимального розподілення кредитних ресурсів банку серед запропонованих бізнес-проектів?
Як побудувати пріоритетний ряд інвестиційного проекту банку?
