Первинна обробка результатiв магнiтометричних спостережень на археологiчних пам’ятках

В.П.Дудкін, М.І.Жарких, І.М.Кошелев

Магнітометричні спостереження часто ускладнені систематичними похибками, які утруднюють використання результатів магнітної розвідки в археології. В статті запропоновано варіант методу найменших квадратів, який дозволяє усунути ці похибки. Метод реалізовано у вигляді програми для персональних комп’ютерів. Можливості методу та прийоми обробки продемонстровано на прикладі трипільського поселення Глибочок (Тальнівський район Черкаської області).

Походження систематичних похибок магнітометричних спостережень

Протягом останньої чвертi столiття для пошукiв та розвiдки археологiчних пам’яток широко застосовують геофiзичнi методи. Найбiльш простим i розповсюдженим є метод магнiтної розвiдки.

Магнiтометричнi спостереження проводять попланшетно по системi паралельних профiлiв з постiйним iнтервалом мiж профiлями та пiкетами. Планшети прямокутної, найчастiше квадратної форми мають розмiри вiд 50×50 до 100×100 м. Пункти магнiтометричних вимiрювань утворюють на мiсцевостi, як правило, рiвномiрну мережу густою вiд 1×1 до 4×4 м. Отже, в межах одного планшету налiчується декiлька сотень або навiть тисяч спостережень.

Археологiчнi пам’ятки, наприклад поселення часiв трипiльської цивілізації, часто займають площу, що складає десятки i сотнi гектарiв. Це вiдповiдає десяткам i сотням планшетiв магнiтометричної зйомки. У цiлому, обсяг магнiтометричних спостережень може бути досить великим, але їхне регулярне розташування на мiсцевостi дозволяє створити зручнi для обчислень масиви даних i для їх обробки широко застосувати сучаснi комп’ютери.

Магнiтометричнi вимiрювання на рiзних планшетах виконують у рiзнi днi, в рiзнi перiоди польового сезону (в залежностi вiд строкiв сiльськогосподарських робiт), а часто i в рiзнi роки. Внаслiдок цього через нестабiльнiсть роботи вимiрювальної апаратури i дiю варiацiй магнiтного поля Землi виникає досить непроста проблема приведення магнiтних спостережень до єдиного рiвня.

Методичнi прийоми магнiтної зйомки (використання опорної мережi, контрольних пунктiв, щоденна реєстрацiя магнiтних варiацiй тощо) у деякiй мiрi вирiшують цю проблему, але далеко не повнiстю, головним чином для груп планшетiв, на яких зйомочнi роботи проводилися без розриву у часi. В рештi випадкiв неузгодженiсть рiвнiв магнiтного поля мiж планшетами може набагато (в десятки разiв) перевищувати похибку магнiтометричних вимiрювань. Це перешкоджає застосуванню комп’ютерної обробки магнiтометричних матерiалiв внаслiдок генерування неiснуючих (хибних) локальних аномалiй на межах сусiднiх планшетiв.

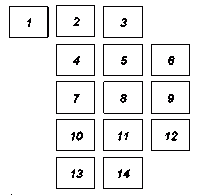
Як приклад можно навести данi по поселенню Глибочок (Тальнівський район Черкаської області), де у 1994 р. проведена магнiтометрична зйомка протонними магнiтометрами з точнiстю 2 нТ на мережi 4×4 м на планшетах розмiром 100×100 м. В 1995 р. зйомка була продовжена (планшети з номерами бiльше вiд 100, рис. 1).

Формальне приведення висхiдних даних безпосередньо по польових журналах до якогось умовного єдиного рiвня (в даному випадку – дo рiвня 49900 нТ) не дає бажаних результатiв. Такi данi iлюструються рис. 2, з якого видно, що висхiдне магнiтне поле зберiгає високу ступiнь неузгодженостi, особливо на межах планшетiв зйомок рiзних рокiв, де рiзниця рiвнiв поля подекуди перевищує 50 нТ. Як показують експерименти, не досягають мети i спроби привести висхiдне поле до єдиного рiвня паралельним змiщенням рiвнiв поля сусiднiх планшетiв на деяку сталу величину. Це означає, що неузгодженiсть полiв окремих планшетiв описується бiльш складним спiввiдношенням i для успiшного розв’язання поставленої задачi треба розглянути бiльш досконалий алгоритм.

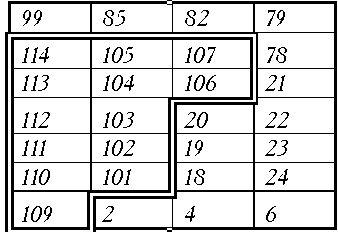
Рис. 1. Схема розташування планшетiв на межi магнiтних зйомок 1994-95 рр. на площi поселення Глибочок. Подвійною рамкою обведено планшети, відзняті у 1995 р.; інші планшети відзняті у 1994 р.

Алгоритм корекції систематичних похибок

Отже, проблема полягає в тому, що магнітне поле (засадничо неперервне) внаслідок систематичних похибок має розриви на межах планшетів (рис. 2). Для усунення цих розривів ми пропонуємо скориґувати магнітне поле шляхом додавання кусково-лінійної функції корекції; її розриви на межах планшетів мають компенсувати розриви висхідного поля. Скориговане поле має вигляд :

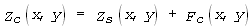(1)

де 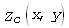– скориговане поле, 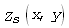– висхідне поле, 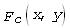– функція корекції; всі ці функції визначені всередині кожного окремого планшету. Функція корекції має вигляд :

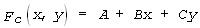(2)

де A, B, C – невідомі коефіцієнти. Для їх визначення ми пропонуємо використати метод найменших квадратів. Величина Q, яка підлягає мінімізації – це сума квадратів змін магнітного поля на межах планшетів :

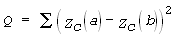(3)

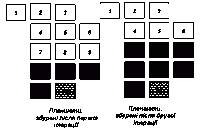
де сума в (3) поширена на лінії стику планшетів, символами a, b умовно позначено сусідні планшети (рис. 3).

Рис. 2. Трипільське поселення Глибочок. Карта висхідного магнітного поля з сильними розривами.	Рис. 3. Трипільське поселення Глибочок. Карта вирівняного магнітного поля, на якій розриви зникли.

Більш формально цю суму можна визначити за допомогою такої формули :

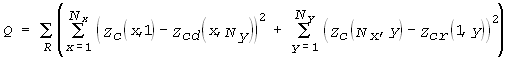(4)

В формулі (4) N_x позначенає число пікетів, N_y – число профілів, R позначечає всю множину планшетів, які мають непустого нижнього або правого сусіда (рис. 4); поле обраного планшета позначене 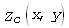; перший член в дужках є сумою квадратів різниць між нижнім профілем обраного планшета та верхнім профілем його нижнього сусіда Z_cd; другий член в дужках є сумою квадратів різниць між крайнім правим рядом пікетів обраного планшета та крайнім лівим рядом його правого сусіда сусіда Z_cr; кожен з цих членів може бути відсутнім, якщо відповідного сусіда нема. Наприклад, для конфігурації планшетів, зображеної на рис. 4, планшет 1 має правого сусіда, та не має нижнього; планшети 2, 4, 5 та інші мають обох сусідів; планшет 3 має тільки нижнього сусіда, не маючи правого.

Сума квадратів (4) залежить від параметрів A, B, C для всіх планшетів; отже, якщо загальне число планшетів є N_p, то потрібно визначити 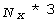невідомих. Для цього можна використати два методи. Перший метод є стандартним для застосування процедури найменших квадратів : треба підставити вираз (2) у формулу (1), а потім результат підстановки – в суму (4). В такий спосіб ми визначимо залежність суми (4) від невідомих параметрів. Далі треба продиференціювати цю суму по всіх невідомих параметрах, щоб утворити систему 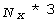лінійних алгебраїчних рівнянь відносно такого ж числа невідомих параметрів. Розв’язавши цю систему стандартними методами лінійної алгебри, ми отримуємо пошукуваний набір параметрів функції корекції. Істотною перевагою цього способу є отримання результатів за один прохід алгоритму; недоліком є складність утворення висхідної суми квадратів і, як результат – дуже складна структура коефіцієнтів рівнянь. Ця складність, спричинена необхідністю обробляти набори з довільним взаємним розташуванням планшетів, є питомою складністю самої постановки задачі і ії не можна оминути.

Другий метод полягає в тому, щоб мінімізувати суму квадратів для одного обраного планшету; її можна записати подібно до (4) :

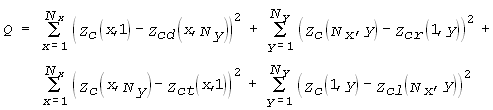(5)

де Z_ct, Z_cl – відповідно значення поля для верхнього і лівого сусідів. Для цього процесу мінімізації сусідні планшети мусять виставляти дані на межах з урахуванням їх власних функцій корекції. Оскільки результат коригування даного планшету залежить від таких же результатів для сусідніх планшетів, необхідно виконувати цикли ітерацій по всіх планшетах. Ознакою досягнення збіжності ітерацій є незначна зміна параметрів функції корекції, отриманих на даному етапі ітерацій, з аналогічним набором із попереднього етапу. Недоліком цього методу є його ітераційний характер (швидкість збіжності може до того ж залежати від порядку виконання ітерацій; наприклад, для рис. 4 це може бути послідовність 1 – 2 – 3… чи 14 – 13 – 12… чи ще якась). Але безперечною перевагою є його ідеальна підпорядкованість вимогам об’єктної декомпозиції. Через це побудова об’єктної програми обчислень на ЕОМ виглядає дуже просто.

Об’єктна реалізація алгоритму

Основним об’єктом реалізації другого з описаних вище алгоритмів є об’єкт “Планшет”. Цей об’єкт має такі властивості :

– він уміє завантажувати дані з файлу;

– він уміє формувати звіти про результати своєї роботи і зберігати їх у файлах;

– він може визначити наявність своїх сусідів;

– він обчислює і повертає значення поля у будь-якій точці своєї границі (це поле може бути або висхідним нескоригованим полем, або полем з урахуванням поточного значення функції корекції даного планшету);

– він обчислює поточний набір параметрів своєї функції корекції;

– він запам’ятовує поточний і попередній набори параметрів своєї функції корекції;

– він порівнює поточний і попередній набори параметрів своєї функції корекції за заданими критеріями.

Запрограмувати такий об’єкт можна за допомогою будь-якої об’єктної мови програмування (в нашому випадку “Планшет” був успадкований від базового об’єкту TView бібліотеки TurboVision 2.0 для мови Pascal). Неформально ці властивості можна описати так. В результаті виконання методу 1 (читання даних) “Планшет” набуває здатності відповідати “я є” на запити, що приходять від інших об’єктів. Якщо дані не завантажені або завантажені з помилками, “Планшет” відповідає “мене нема”. Для обчислення суми квадратів (5) “Планшет” визначає присутність своїх сусідів за допомогою методу 3; після цього сусіди за допомогою свого методу 4 повертають поточному “Планшетові” потрібні йому дані, обчислють коефіцієнти системи 3 лінійних рівнянь і розв’язують її. Так виглядає реалізація методу 5. Для закінчення процесу ітерацій треба опитати всі планшети за допомогою методу 7 : якщо він скрізь повертає значення “істина”, процес ітерацій вважається закінченим.

Аналіз процесу збіжності

Оскільки запропонований нами алгоритм є ітераційним, питання його збіжності треба вивчати. З теоретичної точки зору збіжність процесу ітерацій не підлягає сумніву : оскільки існує єдиний набір параметрів функцій корекції, який забезпечує досягнення мінімуму суми квадратів (4), то цей самий набір буде забезпечувати й досягнення збіжності ітераційного алгоритму. Інша справа – наскільки швидко збігається процес ітерацій і які умови краще поставити для контролю збіжності.

Типовими значеннями поля є 200..300 нТ, причому точність вимірювань цього значення не перевищує 1 нТ. Тому можна вважати, що розбіжність функцій корекції, отриманих на двох послідовних ітераціях (позначимо їх номерами 1 і 2), не повинна перевищувати 2..3 нТ :

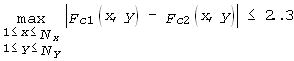(6)

Цю величину похибки можна розділити порівну між усіма трьома параметрами, отримавши для них такі нерівності :

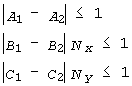(7)

Оскільки типове значення числа пікетів та числа профілів є 20.25, то маємо для останніх двох нерівностей :

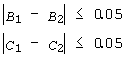(8)

Рис. 5. Приклад взаємного розташування планшетів.	Рис. 6. Поширення збурень в процесі ітерацій.

Процес збіжності може носити хвилеподібний характер, коли параметр в процесі ітерацій кілька разів перетинає свій кінцевий рівень. Це пов’язане з хвилеподібним поширенням збурень функції корекції від кожного окремого планшету. Щоб краще пояснити цю ситуацію, розглянемо випадок рис. 4 і припустимо, що тільки планшет 14 має розриви на межах з іншими планшетами, а ітерації виконуються у послідовності 1 – 2 – 3… Тоді під час виконання першої ітерації всі планшети, окрім найближчих сусідів плантешу 14 (тобто планшетів 10 – 13) залишаться незбуреними – вони, так би мовити, ще не знають про наявність розриву поля. Після виконання другої ітерації збурення пошириться на планшети 7 – 9 (рис. 6). Ітерації в цьому випадку закінчаться коли збурення, внесене планшетом 14, буде скомпенсоване кількома рядами його сусідів.

Рис. 7. Приклад монотонного наближення параметрів корекції до граничних значень (планшет 19).	Рис. 8. Приклад коливального наближення параметрів корекції до граничних значень (планшет 82).

Для того, щоб спростити відстежування за процесом збіжності, програма для ПК має спеціальний режим контролю збіжності. За допомогою цього режиму кожен планшет формує файл зі значеннями параметрів функції корекції для кожної виконаної ітерації. За допомогою цих файлів легко побудувати графіки збіжності, які представлені на рис. 7 – 8. Досвід вивчення процесу збіжності для поселення Глибочок показав, що можна виділити два граничні випадки поведінки :

монотонне наближення всіх параметрів до своїх граничних значень (рис. 7) (зауважимо, що процес ітерацій ми завжди почнаємо з нульових значень параметрів). Ця ситуація є набільш сприятливою для збіжності процесу;

коливальне наближення хоча б одного з параметрів до свого граничного значення. В нашому прикладі спостерігалось не більше трьох екстремумів (рис. 8). Ця ситуація є найменш сприятливою для збіжності процесу.

Для інших планшетів криві мають менше екстремумів і тому можуть розглядатись як такі, що лежать між описаними вище граничиними випадками. Варто відзначити, що навіть в найнесприятливішій ситуації (рис. 8) коливання згасають протягом перших 10 ітерацій і далі процес збіжності протікає монотонно. А ця монотонна збіжність, в свою чергу, дає впевненість у тому, що знайдено справжній глобальний мінімум суми квадратів (3).

Аналіз якості корекції за допомогою функцій розподілу

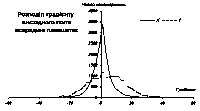
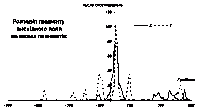
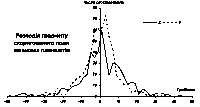
Досить потужним інструментом дослідження якості внесеної корекції є, на наш погляд, вивчення функцій розподілу горизонтального та вертикального градієнтів магнітного поля. Програма окремо вираховує такі гістограми розподілу для магнітного поля всередині планшетів і для поля на межах планшетів. Наявність розривів у висхідному полі приводить до того, що для висхідного поля гістограми розподілу на межах планшетів (рис. 10) не має нічого спільного з такими ж гістограмами для внутрішніх частин планшетів (рис. 9). Якщо градієнт висхідного поля всередині планшетів має розподіл з одним максимумом, який лежить більше-менше в околиці нуля і є симетричним, то розподіл на межах планшетів має кілька максимумів, різко зміщених від нуля.

Рис. 9. Розподіл ґрадієнту висхідного поля посередині планшетів.	Рис. 10. Розподіл ґрадієнту висхідного поля на межах планшетів.
Рис. 11. Розподіл ґрадієнту скоригованого поля посередині планшетів.	Рис. 12. Розподіл ґрадієнту скоригованого поля на межах планшетів.

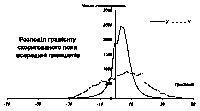
Ситуація кардинально змінюється після внесення корекції. Якщо розподіл по внутрішніх областях планшетів не зазнав кардинальних змін (рис. 11), то розподіл значень на границях (рис. 12) змінився досить відчутно : замість кількох дуже далеких від нуля максимумів ми маємо один максимум поблизу нуля і більш-менш симетричні крила розподілу. Особливу увагу треба звернути на те, що масштаб осі абсцис на рис. 12 у десять разів більший за такий же масштаб на рис. 10, що означає різке зменшення розпорошення ґрадієнтів після корекції. Це означає, що розподіл на границях планшетів дуже наблизився до розподілу посередині планшетів і може розглядатись як вибірка з тої самої генеральної сукупності, що й величини посередині планшетів. Інакше кажучи, статистичні властивості градієнту магнітного поля на межах планшетів після корекції перестали вирізнятись на загальному тлі, а тому межі планшетів не можуть більше бути джерелом хибних об’єктів під час інтерпретації.

Програмна реалізація

Для полегшення комп’ютерної обробки магнітометричних спостережень описаний вище алгоритм був реалізований у вигляді автономної програми GeoFilter 1.0. Ця програма являє собою інтегроване середовище працівника-інтерпретатора, яка працює в середовищі MS DOS. Вона може виконуватись на будь-якому персональному комп’ютері, сумісному з IBM рівня 80286 чи вище. Інтерфейс програми реалізовано у двох варіантах : україномовному і англомовному. Загальний обсяг всіх файлів – біля 300 Кбайт. Швидкодія її досить висока : для використаного нами прикладу (28 планшетів, 17500 спостережень) повний цикл 45 ітерацій були виконано за 10 секунд (на копм’ютері 80486DX2, 66 Мгц).

За допомогою цієї програми працівник-інтерпретатор :

– описує взаєморозташування планшетів та завдає їх зв’язок з файлами висхідних даних;

– кориґує дані, задаваючи різні умови збіжності процесу;

– контролює хід ітерацій за допомогою файлів збіжності;

– формує різноманітні звіти (висхідне поле для всіх планшетів, як на рис. 2; скориговане поле для всіх планшетів, як на рис. 3; дані для побудови функцій розподілу рис. 9 – 12).

Можна сподіватись, що використання цієї програми полегшить обробку магнітометричних вимірювань і підвищить їхню інформативність.

Джерело : Археометрія та охорона історико-культурної спадщини, 1997 р., вип. 1, с. 10 – 18.