4.1. Практичне використання моделі визначення вартості клієнтської бази банку

Трикозенко О. Г., Брітченко І. Г.

Роками фінансові установи проводили політику, направлену на залучення та формування клієнтської бази. Розвинута та стабільна клієнтська база формує необхідну основу розвитку універсального комерційного банку. Комерційні банки виявляють особливу турботу про розширення кола своїх клієнтів і зміцнення відносин з ними. Кожний комерційний банк із року в рік удосконалює свою продуктову базу, розширює мережу своїх відділень, банкоматів та створює умови для постійного нарощення клієнтської бази. Усі ці дії комерційний банк проводить для того, щоб утримати вже наявну клієнтську базу та залучити нових клієнтів. Залучення нових клієнтів до обслуговування в банку – процес важливий, але не складний. Складнішим є питання, як втримати уже наявну клієнтську базу та передбачити прогнозний термін обслуговування клієнтів у банку.

У вітчизняному фінансовому просторі вкладник приймає рішення найчастіше інтуїтивно, реагуючи скоріше на чутки, ніж на факти. Подібна ситуація може стати згубною для будь-якого успішного банку. При цьому досить лише грамотно спланувати поширення негативної інформації про банк конкурента. В умовах, коли одержати об’єктивну інформацію немає звідки, клієнти легко піддаються паніці, а для банку паніка в рядах вкладників – одна із найбільш серйозних проблем.

Для того, щоб зробити правильний вибір, споживач банківських послуг повинен вміти орієнтуватися на ринку, зіставляти послуги різних банків з погляду їх ціни та якості.

Спочатку клієнт може довідатися про банк від друзів, знайомих, колег по роботі, з рекламного оголошення, від працівників самого банку. Вибір банку може бути продиктований тим, що його офіс знаходиться близько до місця проживання клієнта або до місця роботи; банк може пропонувати відносно дешеві послуги; і такі, яких немає в інших місцевих банках, зрештою банк має високу репутацію в місті, районі.

Проведені в різних країнах дослідження мотивів вибору банків клієнтами показують, що на перше місце останні ставлять кількість і якість наданих банком послуг, далі – ціну послуг (наприклад, відсоткові ставки за внесками населення, депозитами, кредитами), швидкість проведення операцій, і лише на останнє місце – те, що клієнт користувався послугами цього банку раніше. Такий порядок мотивів підвищує значення тих чинників, що носять не тільки економічний, але й психологічний характер: час прийому, час очікування, тон звертання та бесіди працівників банку, рівень їх уваги тощо.

Розглянемо основні мотиви, що спонукають клієнта до придбання банківських послуг.

1. Прибуток або економія. Одержання прибутку є важливим мотивом звертання до послуг банку. Для потенційних клієнтів велике значення має рівень відсоткових ставок.

2. Еластичність послуг. Особливою увагою в клієнтів користуються еластичні (гнучкі) послуги, що можуть бути пристосовані до потреб, які змінюються.

3. Якість послуг. При виборі послуг клієнт орієнтується, як правило, на ціну або вартість послуг.

4. Швидкість. Клієнт завжди зацікавлений у підвищенні швидкості надання необхідних послуг і одержанні прибутку.

5. Безпека. Клієнти серйозно зацікавлені в безпеці своїх коштів і прагнуть цілком покладатися на банк у заощадженні внесків.

6. Гарантоване обслуговування.

7. Зручність. Одним із другорядних мотивів при виборі банку є організаційна зручність і/чи вигідність його місцерозташування.

8. Репутація й відчутна технічна майстерність. Це один з найважливіших мотивів як при виборі банку, так і при оцінці доцільності придбання тих чи інших продуктів/послуг конкретного банку.

На жаль, більшість юридичних і фізичних осіб, вперше вибираючи банк або за різних причин змінюючи його, орієнтуються передусім на суб’єктивні чинники (рекламу, особисті зв’язки серед менеджменту банку та ін.) і практично не звертають уваги на об’єктивні фінансові показники банку. Тому найпершим кроком у цьому напрямку має бути хоча б поверхневе ознайомлення з балансами обраних при попередньому відборі банків [48].

Під час залучення або обслуговування клієнта працівнику необхідно добре розуміти, чим керується клієнт, приймаючи рішення про придбання банківських послуг. Фахові якості персонального менеджера, який займається залученням нових клієнтів, містять у собі [12]:

– уміння швидко орієнтуватися і приймати рішення, часто пов’язані з ризиком;

– знання типології людей, основ логіки і психології;

– володіння правилами ділового спілкування й етикету;

– спостережливість;

– володіння власним голосом і правильною мовою;

– оптимістичний погляд на світ.

Усю сукупність можливих мотивів клієнта можна об’єднати в три групи:

• раціональні мотиви;

• емоційні мотиви;

• моральні мотиви.

У групі раціональних мотивів найбільш суттєву роль відіграє економічний мотив (мотив одержання прибутку або економії витрат). Важливими також є мотиви надійності й гарантій, які спрямовані на мінімізацію можливих ризиків, та мотиви зручності й додаткових переваг, які виявляються в рівні якості банківських послуг, сервісу обслуговування, зручності придбання, банківських технологій тощо.

Серед емоційних мотивів насамперед виділяють мотив значущості та самореалізації, зміст якого полягає у цілком природному бажанні клієнта бути визнаним у своєму оточенні, підвищити свій соціальний статус та імідж. Мотив свободи полягає у прагненні отримати певний рівень захисту від можливих негативних обставин у майбутньому. Вибір клієнтами окремих банківських продуктів або їхньої участі в певних програмах банку може бути обумовлений мотивами патріотизму, кохання та іншими емоційними мотивами.

Реальне використання моральних мотивів є можливим тільки щодо банків з бездоганною репутацією, високим іміджем та з чітко вираженою соціальною орієнтацією його діяльності. До основних моральних мотивів можуть бути віднесені:

• мотив справедливості, що полягає у піклуванні про знедолених;

• екологічний мотив, який фіксує орієнтацію банку та його клієнтів на захист навколишнього середовища;

• мотив порядності, що ґрунтується на головних моральних цінностях.

Проведеними маркетинговими дослідженнями встановлено, що вирішальним мотивом вибору клієнтом банку є асортимент і якість послуг, друге місце займає ціна послуг, далі – швидкість здійснення операцій. Будь-який клієнт приймає позитивні рішення про придбання банківської послуги тільки за наявності трьох взаємопов’язаних чинників [79]:

• клієнт явно або приховано має потребу в конкретній послузі;

• ця послуга повинна відповідати уявленням клієнта про її якість;

• вартість послуги повинна задовольняти фінансові можливості клієнта.

Розглянемо ймовірнісні методи оцінки вартості клієнтели. Дискретною називають випадкову величину, можливі значення якої – це відокремлені ізольовані числа (тобто між двома можливими значеннями немає проміжних значень), які ця величина приймає з певними ймовірностями. Іншими словами: значення дискретної випадкової величини можна перенумерувати.

Законом розподілу випадкової величини називають перелік її можливих значень і відповідних ймовірностей [73, с. 359].

де

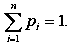(18)

Біноміальним називають закон розподілу випадкової величини – числа появи події у незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює ; ймовірність можливого значення обчислюють за формулою Бернуллі [73, с. 361]:

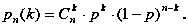(19)

Приклад: комерційний банк видає послугу – 10 кредитів клієнтам на придбання авто. Ймовірність того, що кожен клієнт не поверне кредит дорівнює 0,05. Знайдемо ймовірність того, що рівно два клієнти зовсім не повернуть кредит..

Якщо кількість випробувань достатньо велика, а ймовірність появи події у кожному випробуванні достатньо мала, то використовуємо наближену формулу

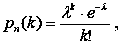(20)

де: k – кількість появи події у випробуваннях;

λ = np – середня кількість появи події у цих випробуваннях. Ця формула називається розподілом Пуассона [28, с. 44].

Пуассоновським потоком подій називають послідовність подій, які мають такі три властивості: стаціонарність, відсутність післядії, ординарність:

• Властивість «стаціонарності» полягає у тому, що ймовірність появи подій у будь-який момент часу залежить тільки від k і від довжини t проміжку часу й не залежить від початку його відліку. Іншими словами, ймовірність появи k подій за проміжок часу t є функцією, яка залежить лише від k і t.

• Властивість «відсутності післядії» полягає в тому, що ймовірність появи k подій у будь-якому проміжку часу не залежить від того, з’являлись чи не з’являлись події в моменти часу, що передували початку проміжку, що розглядається. Іншими словами, передісторія потоку не впливає на ймовірності появи цих подій у найближчому майбутньому.

• Властивість «ординарності» полягає в тому, що поява двох або більшої кількості подій за малий проміжок часу практично неможлива. Іншими словами, ймовірність появи більше однієї події за достатньо малий проміжок часу значно менша за ймовірність появи рівно однієї події.

Інтенсивністю потоку λ називають середню кількість подій, які з’являються за одиницю часу [91].

Теорема 1. Ймовірність появи подій за час можна визначити за формулою

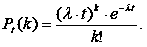(21)

Доведення: треба довести, що наведена формула відображає всі властивості Пуассонівського потоку [20, с. 61].

Із формули (21) ми бачимо, що ймовірність появи k подій за час t при заданій інтенсивності λ є функцією від k і t, що підтверджує властивість стаціонарності.

Формула (21) не використовує інформації про появу подій до початку моменту часу, що розглядається. Таким чином, властивість «відсутності післядії» виконується.

Покажемо, що формула (21) задовольняє властивість ординарності. Покладемо: k = 0 і k = 1. Знайдемо ймовірності непояви події та появи цієї події один раз.

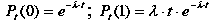(22)

Отже, ймовірність появи події більше одного разу:

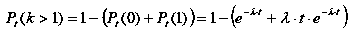(23)

Використаємо формулу Маклорена для розкладу функції y = e^x у степеневий ряд [22, с. 368].

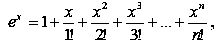
отримаємо:

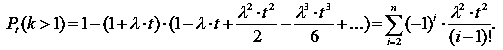(24)

Аналіз отриманого функціонального ряду уможливлює зробити висновок, що при достатньо малих проміжках часу виконується нерівність P_t(k = 1) >> P_t(k > 1). Отже, зазначена формула характеризує всі три властивості Пуассонівського потоку. Теорему доведено. Зауважимо, що формула (24) дає можливість оцінити ймовірність втрати клієнта під час прецесійної фази економічного циклу.

Математичним сподіванням дискретної випадкової величини є скалярний добуток значень X на відповідні їм ймовірності, тобто [73, с. 362]

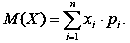(25)

Дисперсією дискретної випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання [73, с. 362].

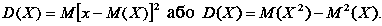(26)

Висновок: маючи можливість знаходити математичне сподівання та дисперсію за даними дискретної випадкової величини (кількість клієнтів, сума кредитів, суми депозитів), можемо оцінити вартість клієнтели в часі з певною ймовірністю. Урахувавши всі ці показники, можна зробити розрахунки, які допоможуть визначити вартість клієнтели. Важливим моментом при цьому підході є те, що оцінка вартості відбувається з урахуванням майбутніх ризиків.

Теорема 2 (про математичне сподівання розподілу Пуассона).

Математичне сподівання дискретної випадкової величини, яка задана розподілом Пуассона, дорівнює параметру цього розподілу.

Доведення: розподіл Пуассона можна задати за допомогою таблиці: [28, с. 48].

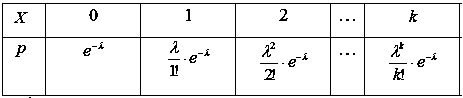
За означенням математичного сподівання (число можливих значень – злічена множина):

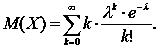(27)

Ураховуючи, що при k = 0 перший доданок суми дорівнює нулю, приймаємо за найменше значення k одиницю і виносимо за знак суми множники, що не залежать від k:

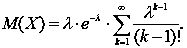(28)

В останньому виразі покладемо: k – 1 = m, отримаємо:

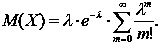(29)

Оскільки

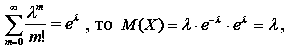
що й треба довести.

Висновок: надалі буде показано, що Пуассонівський закон підпорядковується оцінці вартості клієнтели під час піднесення та рецесії на фазах ділового (економічного) циклу.

Теорема 3 (про дисперсію розподілу Пуассона).

Дисперсія дискретної випадкової величини, яка задана розподілом Пуассона, дорівнює параметру цього розподілу.

Доведення: скористаємось формулою D(X) = M(X²) – M²(X) і теоремою 2.

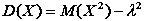(30)

Запишемо розподіл випадкової величини X², ураховуючи, що ймовірність того, що випадкова величина X² дорівнює k², дорівнює ймовірності того, що випадкова величина X дорівнює k (це випливає з того, що можливі значення невід’ємні) [28, с. 51].

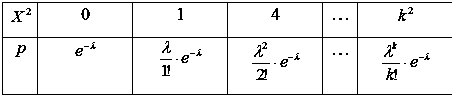
Знаходимо математичне сподівання X²:

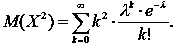(31)

Враховуючи, що перший доданок суми дорівнює нулю, маємо:

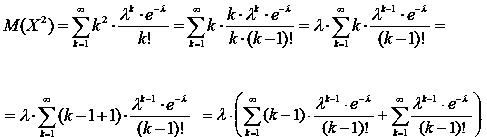(32)

Покладемо k – 1 = m:

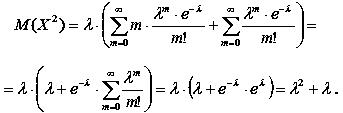(33)

Остаточно маємо: D(X) = λ² + λ – λ² = λ, що й треба довести.

Нерівність Чебишева [28, с. 109].

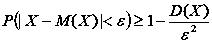(34)

Приклад. Нехай подія A – полягає у тому, що до банка звертається клієнт з приводу депозитного вкладу. Ймовірність появи події A дорівнює p (тобто, з ймовірністю p клієнт робить вклад і з ймовірністю 1 – p він свій вклад не робить). Припустимо, що за певний період часу (наприклад, один місяць) до банку звернулося N клієнтів. Необхідно оцінити, що кількість клієнтів, які зроблять свої вклади, перебуває у межах від a до b.

Розв’язання:

Знаходимо математичне сподівання і дисперсію випадкової дискретної величини X – числа появи події A для N клієнтів.

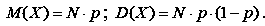(35)

Знаходимо модуль максимальної різниці між математичним сподіванням і заданим числом появи події A.

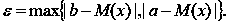(36)

Тоді

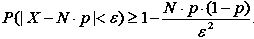(37)

Припустимо, що за певний період часу до банку звернулося 100 клієнтів. Ймовірність того, що кожен клієнт зробить депозитний вклад p = 0,3. Оцінити можливість того, що кількість клієнтів, які зроблять вклади, лежить у межах від 20 до 40.

У цьому випадку: N = 100, a = 20, b = 40, тоді M(X) = 100 × 0,3 = 30; ε = 10;

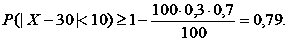
Нормальним називають розподіл випадкової величини , якщо щільність цього розподілу задана формулою

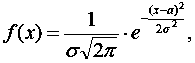(38)

де:

σ – середнє квадратичне відхилення;

a – математичне сподівання.

Ймовірність того, що X приймає значення, яке належить інтервалу (α, β) – знаходимо за формулою

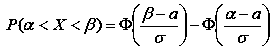(39)

де 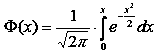– функція Лапласа. Функція Лапласа не інтегрується у квадратурах, тобто не можна знайти елементарну функцію, яка виражала б інтеграл 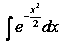. Значення функції Лапласа можна знайти в теоремі 4 [19, с. 389].

Для нашого прикладу, якщо треба знайти ймовірність того, що не менше 50 клієнтів відкриють депозитні рахунки, то

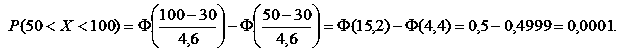
Якщо ж треба знайти ймовірність того, що клієнтів буде від 20 до 40, отримаємо:

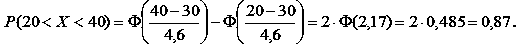
При обчисленні було використано важливу властивість функції Лапласа.

Висновок: отримано метод, за допомогою якого можна оцінити кількість клієнтів, котрі припинять свої стосунки з комерційним банком, або кількість потенційних, нових клієнтів, які розпочнуть свої стосунки з фінансовою установою.

Теорема 4 Функція Лапласа – непарна.

Доведення.

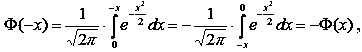(40)

що й треба довести.

Зробимо важливе зауваження. Оцінка за нерівністю Чебишева дає лише нижню оцінку можливої ймовірності (ймовірність не може бути МЕНШОЮ за 0,79). Використання формули, яка містить функцію Лапласа, дає більш точну оцінку. Абсолютна похибка оцінки не перевищує 0,01% (тобто похибка з’являється тільки на четвертому символі після коми).

Показниковим (експоненціальним) розподілом називають розподіл ймовірностей неперервної випадкової величини , яке описується щільністю

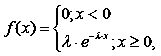(41)

де λ – стала величина [19, с. 114].

Функція розподілу показникового розподілу:

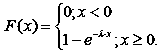(42)

Ймовірність потрапляння випадкової величини, яка розподілена за показниковим розподілом в інтервал , дорівнює

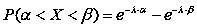(43)

де: P – ймовірність;

α – ліва межа;

X – випадкова величина;

β – права межа.

Висновок: показниковий розподіл є важливим елементом оцінки витрат та доходів виробничого підприємства. Він дає змогу оцінити такі важливі показники, як рентабельність та прибутковість.

Теорема 5 Математичне сподівання, дисперсія та середнє квадратичне відхилення показникового розподілу дорівнюють:

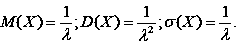(44)

Доведення: використовуємо формулу 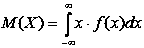. Оскільки f(x) = 0 для x < 0, то

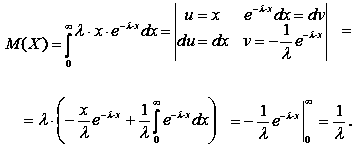(45)

Для знаходження дисперсії використаємо формулу:

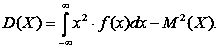(46)

Для знаходження інтегралу 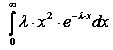двічі використовуємо формулу інтегрування частинами. Маємо: 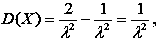, звідки .

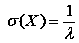Висновок: на фазах економічного циклу – депресія та бум (піднесення) – оцінка вартості клієнтели підпорядковується показниковому розподілу. Знаючи дисперсію цього розподілу, ми можемо зменшити оцінку похибки у вартості клієнтели до 2 відсотків (тобто реальна вартість стане не більшою, або не меншою 2 відсотків).

Теорема 6 Неперервна випадкова величина T – час між появою двох послідовних подій пуассонівського потоку із заданою інтенсивністю λ – має показників розподіл:

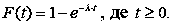(47)

Доведення: припустимо, що в момент t₀ настала подія потоку. Нехай t₁ = t₀ + t.

Якщо хоча б одна подія потоку, що йде за подією A₁, відбудеться в інтервалі, що міститься в (t₀; t₂), де t₀ < t₂ < t₁, то час T між появою двох послідовних подій виявиться меншим за t, тобто T < t.

Для того, щоб знайти ймовірність P(T < t), врахуємо, що події – «в інтервалі (t₀; t₁) відбулася хоча б одна подія з потоку» і «в інтервалі (t₀; t₁) не відбулося жодної події з потоку» протилежні (сума ймовірностей цих подій дорівнює одиниці).

Ймовірність непояви жодної події з потоку за час дорівнює

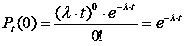(48)

Тоді ймовірність, що нас цікавить (ймовірність протилежної події), P(T < t) = 1 – e^λt, або за визначенням функції розподілу F(t) = 1 – e^λt при t ≥ 0. Що й треба довести.

Висновок: розглянуті теореми в цьому питанні дають можливість за допомогою математичного аналізу оцінювати вартість клієнтели через повний проміжок часу з певною (розрахованою за допомогою методів, що описані вище) ймовірністю.

Функція надійності. Клієнт як складова частина, що впливає на розвиток фінансової установи, займає важливе місце. У першому розділі ми вже чітко обгрунтували той факт, що клієнтська база комерційного банку є його нематеріальним активом. У той час, коли інвестор вирішив придбати собі нову кредитну установу в іншій країни, він повинен добре проаналізувати весь бізнес й особливо приділити увагу клієнтській базі, що на теперішній час обслуговується в банку.

На момент придбання комерційного банку інвестор отримує все, що належить комерційному банку його філіальній мережі, враховуючи всю клієнтську базу. Однак не слід забувати про те, що розвиток філіальної мережі проходить протягом великого проміжку часу. За цей час банк завдяки своїм рекламним кампаніям виходить на новий ринок та залучає нових клієнтів, створюючи свою постійну клієнтську базу. Залучення до банку великої кількості клієнтів – це довгий і трудомісткий процес. У результаті залучення необхідної кількості клієнтів перед маркетинговим відділом постає нове завдання, як їх утримати в банку.

Сьогоденна криза в країні, яка розпочалася 2008 року, сильно вплинула на стратегію роботи комерційних банків. Багато хто з них призупинив подальший розвиток і зайняв очікувальну позицію. Зараз комерційним банкам необхідно стримати відплив клієнтів, тим самим утримавши їхні ресурси на своїх рахунках. А отже, це і є проблемою, яку необхідно розв’язати, розробляючи нові рекламні кампанії. У процесі придбання комерційного банку інвестор повинен проаналізувати клієнтську базу цієї фінансової установи для того, щоб отримати прогнозний результат її втрати. Кожний потенційний інвестор, що придбає новий комерційний банк, може постати перед проблемою недовіри клієнта до нового власника, що у свою чергу призведе до стрімкого зменшення кількості постійної клієнтської бази.

Клієнти мають неабияку цінність для компанії хоча б тому, що, по-перше, вони купують певні товари чи сервіси, а по-друге, можливо, будуть продовжувати купувати ці товари та сервіси у майбутньому. І саме другий аспект повинен стати фокусом та метою, до якої буде прагнутибанк.

Ймовірність того, що теперішній клієнт продовжуватиме користуватися вашими товарами та послугами у майбутньому, залежить від кількох чинників:

• розмір та інтенсивність повідомлень, які надсилаються йому сьогодні і будуть надсилатися в майбутньому;

• ступінь корисності цих повідомлень для споживача;

• ступінь легкості звернення клієнта до банку в разі потреби;

• ступінь чіткості та вправності роботи банку із рахунками;

• відчуття турботи споживачів про себе, чи навпаки – байдужості з боку банку;

• ступінь легкості знаходження потрібної клієнтам інформації на Веб-сайті банку та легкості формування замовлення;

• якість підтримки та сервісу яку пропонує банк;

• швидкість відповіді на електронні та телефонні повідомлення з боку банку.

На поведінку клієнта впливає майже все, що відбувається з ним та фінансовою установою в якій він обслуговується.

А це, у свою чергу означає: що банк би не робив – він або створює або ж навпаки – руйнує стосунки зі своїми клієнтами. Йдеться про так званий „споживацький досвід” – досвід, який споживачі отримують, коли працюють із компанією. Існує безліч прикладів діяльності компаній, яка забезпечувала короткострокове підняття продажу, але водночас руйнувала „споживацький досвід”. Наприклад, нав’язлива комунікація, або ж комунікація, яка не приносить користі споживачеві, може зруйнувати стосунки та знизити цінність клієнта для компанії [123].

Тому ми намагаємося розробити концепцію того, як можна спрогнозувати приблизний відсоток відпливу клієнтів з метою отримання повної картини того, скільки клієнтів залишиться і чи буде цієї кількості достатньо для нормального функціонування комерційного банку деякий час. Отримавши такі дані, інвестор зможе спрогнозувати наступні свої дії.

Тим часом повернемося до питання надійності клієнтської бази банку [35, с. 340]. Розглянемо наочний приклад цієї ситуації.

Приклад. Нехай клієнт починає співпрацювати з банком у момент часу t₀, а в момент часу t – відмовляється від співпраці. Позначимо через T – неперервну випадкову величину – довжину часу, протягом якого клієнт обслуговується в банку, а через λ – інтенсивність відмов від співробітництва (середня кількість відмов за одиницю часу, наприклад, за один місяць).

Довжина часу, протягом якого клієнт співпрацює з банком, має пуассонівський розподіл, що має функцію розподілу

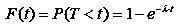(49)

яка визначає ймовірність відмови клієнта за час t.

Функцією надійності R(t) назвемо функцію безвідмовної співпраці клієнта з банком за час : R(t) = e^-λt.

Теорема 7 (характеристична властивість функції надійності).

Ймовірність безвідмовної співпраці клієнта з банком у часовому інтервалі довжини t не залежить від часу співпраці, що передував початку цього інтервалу, а залежить тільки від довжини t (при заданій інтенсивності відмов λ).

Доведення. Введемо позначення подій: A – безвідмовна співпраця клієнта в інтервалі (0; t₀) довжини t₀; B – безвідмовна співпраця клієнта в інтервалі (t₀; t₀ + t) довжини t.

Тоді AB – безвідмовна співпраця в інтервалі (0; t₀ + t) довжини t₀ + t.

За формулою R(t) = e^-λt знайдемо ймовірності цих подій.

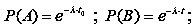	(50)
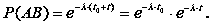	(51)

Знайдемо умовну ймовірність того, що клієнт буде співпрацювати в інтервалі (t₀; t) за умови, що він співпрацював в інтервалі, що йому передував

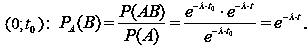(52)

Оскільки в отриманій формулі не міститься t₀, а міститься лише t, то це й означає, що час співпраці в попередньому періоді не впливає на ймовірність співпраці в майбутньому. Іншими словами, умовна ймовірність P_A(B) безвідмовної співпраці в інтервалі часу довжини t, яка обчислена в припущенні, що клієнт безвідмовно співпрацював на попередньому часовому інтервалі, дорівнює безумовній ймовірності P(B).

Висновок: вивчаючи питання надійності клієнтели, було отримано важливий математичний результат – знайдено закон, згідно з яким можна оцінити ймовірність повного припинення клієнтом співпраці або розірвання договірних стосунків з комерційним банком. Такий метод дає змогу робити прогнозний аналіз втрати постійного клієнта.

Практичний алгоритм оцінки вартості клієнтели має такий вигляд:

1. Робимо статистичну оцінку клієнтели.

2. Знаходимо незміщену оцінку генеральної середньої (вибіркова середня).

3. Записуємо закон розподілу випадкової величини (втрата чи невтрата клієнта, у разі невтрати – збільшення чи зменшення фінансової потужності).

4. З’ясовуємо, у якій фазі економічного циклу перебуває економіка (як наслідок – банківська система).

5. У разі рецесії використовуємо пуасонівський закон для оцінки ймовірності втрати клієнтели, у разі піднесення – нормальний закон.