4.2. The mathematical equation

V. I. Melnikov

It is hard to imagine something more common and unquestionable for a modern specialist in any field of knowledge, than displaying (coding) some physical, chemical, financial or any other process as a mathematical equation.

It became so common that we have forgotten that behind every term of an equation, signs between them, real objects and processes that submit common nature laws are ciphered. We are not thinking also about why they are combined in equations not in another form of multitude of quantities and acts. Though, in principle, other multitudes like, for example lines, tables (matrixes), graphic dependences, graphics, tensors, integrals etc. are known, but mathematical equations take in mathematics and all its supplements a particular place.

Basic characteristics and peculiarities of equations and their structures are:

1. Interdependence of quantities.

2. Absence of other factors that are not included in the equation that influence on them.

3. Terms of equation are combined by signs that mean acts.

4. Equal and opposite by a sign terms can be eliminated without upsetting rightness and correctness of an equation.

5. A combination of quantities in the left and right parts can be arbitrary, but their whole amount is always equal to zero.

6. An assemblage of term of an equation is a closed system, so all parts of a CS are obligatory.

So, it is obvious that a mathematical equation is a main model of real CS, which consists of an assemblage of all its parts. These parts cam be stable or changeable, i.e. depending on other parts, known or unknown, compound or simple.

There is no complete similarity between this model and real elementary RCS. In particular, as a rule, there is no process of level rapprochement, though dependence like А –> 0 with t –> ∞ displays exactly this process. Besides, there is no clear functional division (structuring) of different parts and terms of an equation. All of them are equal, although transformation of an equation relative to one of terms means its functional privilege.

Depersonalization (i.e. formalization) of terms hampers a lot an intuitive and heuristic control on behavior of the system. At the same time it can show conditional character of functional division of its parts.

Every equation is only approximation to reality, precise enough for practice. It is a powerful mean for salvation of various problems, as a matter of fact it presents the same CS, but written down in other way.

By the way, formal possibilities of equalization of any equations that are equal to zero and contain terms of any kind, means equality and equivalence of all ACS. Mathematical zero is a model of CS that displays absence of external interaction with other objects or systems, including informational interaction.

Equation solution is interpreted as a reduction of a compound system that consists of great amount of different parts, to a simple system that consists of a sought for object and an equated anti-object with opposite direction of act, which consists of many inner parts of lower hierarchic level.

Possibility of an equation composition is defined by limited possibilities of quantity experimental measurements of concrete parameters of real objects with a set up permissible error. The laws of natural science that are the basis of an equation are approximate as well.

So, a mathematical equation is a rather approximate model of closed system, the exactness of which can be unrestrictedly grown by elimination of the described errors. The limit of exactness is the expediency of necessary exactness, including cost of model setting. As an example we will give a well-known equation of irregular straight-line motion:

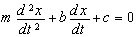
where m is a body mass; x – position of a body in an inertial frame of reference; t – time; b – coefficient of viscous resistance; c – constant power.

As far as all the terms of equation equals zero, this expression presents a model of closed system that expresses motion of a real body (mass) that is in a closed system. Besides a body it includes a viscous medium (coefficient “b”) and a source of constant power “c”. While analyzing a concrete real system, for example a speeding up car, it appears, that all the constants and variables of an equation are approximate. So, a mass of a car can be defined only approximately with great assumptions. The most exact car weighing-machines of open type are 1 to 2 kg exactness. Mass of a car is being minuend during fuel burning.

Speeding up 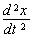is also very approximate because of errors in practical definition of “x” coordinate and the time.

A coefficient of viscous resistance (for example of viscous rut and resistance of head air) is also very indeterminate, approximate and variable in time and space (depth and consistence of mud, position of wheels in a rut, direction and speed of wind, position of a car relative to a rut etc. are changeable). The tern c that was taken as a constant quantity can be for example, a frictional force of wheels, a part of gravitational force of a car. But these forces, from the one hand, cannot be exactly defined, from the other hand they depend on plenty of other factors and are changeable (a slope of a road, quality of roadway covering, state of tires etc. are changing). Besides, a reactive force of exhaust gases, some lunar gravitation, centrifugal forces of Earth’s revolution, light power etc. influence a car.

All these factors cannot be taken into account in a given equation of uniformly accelerated motion.

So, in the presence of full structural and functional similarity of a mathematical equation and a closed system, a basic difference is proximity of a model and statistic character of it (without interaction of its different parts).