4.2. Математическое уравнение

Мельников В.И.

Трудно представить себе что-либо более привычное и неоспоримое для современного специалиста любого профиля, чем представление (или кодирование) какого-либо физического, химического, технического, финансового или любого другого процесса в виде математического уравнения.

Это стало настолько обычным, что мы давно забыли, что за каждым символом, членом уравнений, знаками, соединяющими эти члены, зашифрованы вполне реальные объекты и процессы, подчиняющиеся общим законам природы. Не задумываемся мы и над тем: а почему, собственно, при решении задач они объединяются в основном в уравнение, а не в какую-то другую форму множества величин и действий? Хотя, в принципе, известны другие множества, например ряды, таблицы (матрицы), графические зависимости, графы, тензоры, интегралы и т.д., но математические уравнения занимают в математике и во всех ее приложениях особую роль.

Основные свойства и особенности уравнений и их структуры.

1. Взаимная зависимость друг от друга входящих величин.

2. Отсутствие других, влияющих на них факторов, не входящих в данное уравнение.

3. Члены уравнения соединены знаками, означающими действия.

4. Одинаковые и противоположные по знаку члены уничтожаются без нарушения правильности и корректности уравнения.

5. Сочетание величин в левой и правой частях может быть произвольным, но общая их совокупность всегда равна нулю.

6. Совокупность членов уравнения представляет замкнутую систему, т.е. обязательно наличие всех частей ЗС.

Таким образом, очевидно, что математическое уравнение является знаковой моделью реальной ЗС, состоящей из совокупности всех ее взаимодействующих частей. Эти части могут быть постоянными и переменными, т.е. зависящими от других частей, известными и неизвестными, сложными и простыми.

Полного подобия этой модели и реальной элементарной УЗС нет. В частности, как правило, нет процесса сближения уровней, хотя зависимость типа А –> 0 при t –> ∞ отражает именно этот процесс. Кроме того, нет четкого функционального разделения (структурирования) различных частей и членов уравнения. Они все равнозначны, хотя преобразование уравнения относительно одного из членов означает какое-то его функциональное выделение.

Обезличивание (т.е. формализация) слагаемых существенно затрудняет интуитивный и эвристический контроль за поведением этой системы. Одновременно это говорит об условности функционального разделения его частей.

Любое уравнение является лишь каким-то приближением к реальности, с достаточной для практики точностью. Оно является мощным средством решения самых разных задач, по сути, представляет ту же ЗС, но записанную в другой форме.

Кстати, формальная возможность приравнивания между собой любых приведенных к нулю уравнений, содержащих члены любой природы, означает равноправие и равнозначность всех АЗС. Математический ноль – это модель ЗС, отражающая отсутствие ее внешнего взаимодействия с другими объектами или системами, включая информационное взаимодействие.

Решение уравнения интерпретируется как сведение сложной системы, состоящей из множества различных частей, к простой, состоящей из искомого объекта и приравненного к нему с противоположным по направлению действия антиобъекта, состоящего из множества внутренних частей более низкого иерархического уровня.

Возможность составления уравнения определяется ограниченными возможностями количественных экспериментальных измерений конкретных параметров реальных объектов, с заранее установленной допустимой погрешностью. Приближенными являются и законы естествознания, положенные в основу составления уравнения.

Таким образом, математическое уравнение является весьма приближенной моделью замкнутой системы, точность которой можно неограниченно увеличивать, устраняя указанные виды погрешностей. Пределом точности является практическая целесообразность необходимой точности, включая стоимость составления модели. В качестве примера приведем общеизвестное уравнение неравномерного прямолинейного движения:

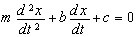
где m – масса тела; х – положение тела в инерциальной системе отсчета; t – время; b – коэффициент вязкого сопротивления; с – постоянная сила.

Поскольку все члены уравнения приравнены нулю, это выражение представляет собой модель замкнутой системы, отражающую движение какого-то реального тела (массы), находящегося в замкнутой системе. Кроме тела в нее входит какая-то вязкая среда (коэффициент «b») и источник постоянной силы «с». При анализе конкретной реальной системы, например, ускоренно движущегося автомобиля, оказывается, что все постоянные и переменные уравнения приблизительны. Так, массу автомобиля можно определить только приблизительно с большими допущениями. Самые точные автомобильные весы открытого типа имеют точность до 1–2 кг. Масса автомобиля по мере сгорания топлива уменьшается.

Ускорение 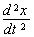также очень приблизительно из-за погрешностей в практическом определении координаты «х» и времени. Коэффициент вязкого сопротивления (например, вязкой колеи и сопротивления встречного воздуха) также оказывается очень неопределенным, приблизительным и переменным как во времени, так и в пространстве (непостоянная глубина и консистенция грязи, положение колес в колее, направление и скорость ветра, положение автомобиля относительно дороги и т.д.). Принятый за постоянную величину член с может быть, например, силой трения колес о дорогу, составляющей силы тяжести автомобиля. Но эти силы, с одной стороны, не могут быть точно определены, а с другой – они зависят от множества других факторов и являются переменными (меняется уклон дороги, качество дорожного покрытия, состояние протекторов шин и т.д.). Кроме того, на автомобиль действует реактивная сила струи выхлопных газов, какое-то притяжение луны, центробежные силы от вращения Земли, световое давление и т.д. и т.п.

Все эти факторы приведенным классическим уравнением равноускоренного движения не учитываются.

Таким образом, при наличии полного структурного и функционального подобия математического уравнения и реальной замкнутой системы принципиальным отличием является грубая приближенность модели и статический (без взаимодействия различных членов между собой) характер ее представления.