3.7. Mass defect
V. I. Melnikov
The relationship between the mass defect and the binding energy is one of the fundamental relationships in modern physics, especially in nuclear physics. Weizsäcker (1935) was the first to propose a quantitative and sufficiently accurate description of this relationship which can be applied to the structures and interactions of the nuclei in the ground state. This description was primarily based on the droplet nuclear model, with the Coulomb repulsion forces, symmetry energy, and the coupling effect taken into account.
However, the droplet nuclear model does not take into account a great body of contemporary experimental data. To this end, we have to resort to a greater number of nuclear models, and each of them can explain only the limited number of the known phenomena.
So, the above-mentioned relationship requires other alternative analytical representations with another physical content.
The degree of agreement between theoretical estimates and experimental results (or the maximum allowable deviation) can serve as the appropriate criterion for the preferable model choice when there is correspondence in the physical content of the model. At first glance the Weizsäcker formula seems to be quite correct in this regard. We can point out at least two underlying reasons.
Firstly, the relationship under investigation is not affected by the effects which are not taken into account by the droplet model (Coulomb forces, symmetry energy, and coupling effect).
Secondly, the accuracy of the formula is secured to some extent by matching the theoretical and experimental dependences with the use of adjustable coefficients. So, the Weizsäcker formula may represent some kind of series expansion of the experimental dependence. In other words, the imperfections of the droplet nuclear model might be compensated by a purely mathematical trick.
The first possible cause does not have solid grounds because the droplet model fails to explain many known phenomena. Moreover, the accuracy of the Weizsäcker formula can be secured only using the assumption of nuclear saturation, according to which the internucleonic forces inexplicably change their direction with distance. The saturation property contradicts the fact of the existence of magic nuclei (which is taken into account in the nuclear shell model) as well as the main points of the rotational model. In these models the nucleus is considered as a unique system with general structure.
Therefore, other representations of the relationship between the mass defect and the binding energy are quite possible. They can use other, alternative, nuclear models. In this respect the “canonization” of the Weizsäcker formula misrepresents the structural and functional properties of nuclei and suppresses the development of other nuclear models.
Furthermore, a sufficiently accurate dependence of the mass defect on mass number can be obtained on the basis of the model of the generalized physical process (Sec. 3.2) without the use of the binding energy concept. In this case the binding energy is interpreted as the interaction intensity or energy. The model of the generalized physical process (hereafter referred to as model) allows one to construct broad generalizations of various physical processes. Such generalizations can include the elaboration of new nuclear models, and their validity can be judged from the degree of coincidence of the theoretical and experimental dependences.
According to our model, mass is considered as the index of the intensity of the hypothetic “mass” interaction between a physical body and the surrounding physical vacuum (Sec. 3.3). This viewpoint allows various experimental facts related, in particular, to the mechanism of generation of gravitational and inertial forces, to the second TSR postulate, etc. to be explained in the context of the unified approach (Secs. 3.3 and 3.4). Let us consider the mass defect problem in the framework of this model.
The mass interaction of a single nucleon with the surrounding media and the mass interaction of a system of nucleons in a nucleus with their surrounding medium go on under different conditions and, therefore, should have different manifestations.
For a single nucleon, the interaction medium includes physical vacuum and interaction products. In the case of isotropic medium, the interaction flow extends uniformly in all directions, and it is characterized by the largest possible cross section. In this case the flow propagates at minimum resistance.
For a nucleon located in a nucleus, the interaction medium includes physical vacuum, interaction products, and other nucleons located in the same nucleus. These additional nucleons interact with their media as well. Since such a system of nucleons occupies a bounded region, the cross section of each flow produced by the nucleons and directed away from the nucleus to the surrounding vacuum decreases by a factor multiple to the number of nucleons. As a result, the resistance to the flow propagation becomes larger, and the interaction intensity decreases. So, the mass of each nucleon in a nucleus is smaller than the mass of a single nucleon. Let us refer to such an interaction as to the spatial interaction (Fig. 17b).
Furthermore, the nucleons in a nucleus interact with one another, and their properties change. These changes, in their turn, are expected to affect the mass interaction process itself. The larger the number of the nucleons and the number of nucleon-to-nucleon bonds, the stronger is their effect on the interaction process. So, the interaction intensity (and, correspondingly, the mass) depends on the number of nucleons as well. Let us refer to such an interaction as to the internucleonic interaction (Fig. 17a). The internucleonic mass interaction is likely to be a part of the strong nucleon-nucleon interaction.
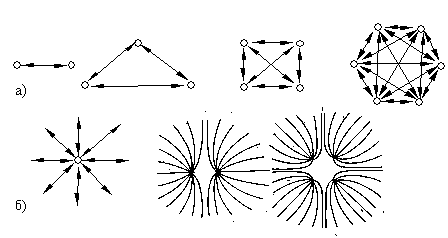
Fig. 17. The sketch of interaction flows in the case of (a) internucleonic interaction and (b) spatial interaction.
The total number of nucleons, their kind, and their mutual arrangement (in particular, the distance between individual nucleons) is of essential significance. The effect of closely located nucleons is stronger. Random factors which depend on the asymmetry of individual nucleons are averaged out at large atomic numbers.
The above-described hypothetic phenomenological picture of the interaction of nucleons with their media correlates, to a first approximation, with the empirical dependence Δ/А.
Let us calculate the mass defect in the case of internucleonic interaction. In a nucleus with A nucleons, each nucleon can interact with other (A – 1) nucleons. The total number of internucleonic bonds (or interaction directions) is equal to A(A – 1). So, the mass defect caused by the internucleonic interaction is
,
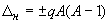where q is the dimensional coefficient of proportionality (mass or energy). The saturation property is evidently excluded.
In the case of spatial interaction, the nucleus is considered as a system of identical parallel sources which direct their interaction flows simultaneously along a single channel extending in the medium surrounding the nucleus. In this case the medium not only takes its part in the interaction but also plays the role of a flow conductor characterized by some resistance.
The resistance of an elementary spherical shell with radius r and thickness dr is
,
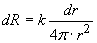where k is the dimensional coefficient of proportionality.
The resistance of the whole ball-shaped medium is
.
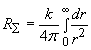The cross section of the medium conducting the flow of one nucleon in the case of a nucleus with A nucleons with the same interaction level U is A times smaller than in the case of an individual nucleon, the medium resistance being A times greater. So, the resistance of the ball-shaped medium formed by the nucleus consisting of A nucleons is
.
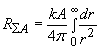The corresponding interaction flow intensity is
,
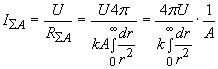while the interaction intensity for a single nucleon is
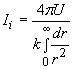
The aggregate interaction flow for A individual nucleons is
.
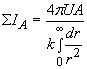The interaction flow difference and, correspondingly, the mass defect are calculated as
.
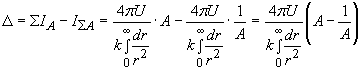Thus, the mass defect caused by the spatial interaction can be written as
,
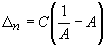where C =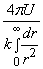 
is the dimensional coefficient of proportionality (mass or energy).
The total mass change caused by the both interactions is
 |
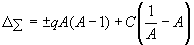(26) |
The empirical dependence Δ/А demonstrates that the internucleonic interaction does not suppress but initiates the mass interaction. So, the first term of relation (26) should be positive. According to the empirical dependence, we have ΔΣ = 0 at A = 216 and ΔΣ = –73.03 MeV at A = 75. By substituting these estimates to expression (43), we derive a system of two equations from which we obtain C = 1.484 · 10-3 MeV and q = 6.9 · 10-3 MeV. Thus, the empirical dependence Δ/А can be represented by the following semi-empirical expression
 |
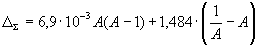(27) |
where ΔΣ is the mass defect in MeV.
|
|
|
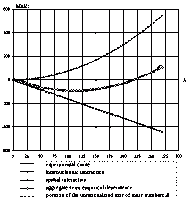
Fig. 18. Mass defect as a function of mass number |
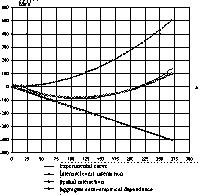
Fig. 19. Mass defect as a function of mass number in the rationalized frame |
Figure 18 shows the corresponding dependences. The deviation of our semi-empirical dependence from the experimental dependence is larger at small mass numbers.
The discrepancies can be diminished if we reduce our semi-empirical dependence to the frame in which the atomic unit is taken equal to the mass of the hydrogen isotope 1H1 (rather than to one-twelfth of the mass of the isotope 12C, whose nucleus contains 12 nucleons). Since this isotope contains only one nucleon, it has no initial mass defect, according to our model (in this case the mass defect can originate only for a group of several nucleons). This new frame is the frame rationalized with respect to the original frame.
The corresponding rationalized axis of mass numbers is shifted by 7.289 MeV in the positive direction, according to the experimental dependence (Fig. 19). In the rationalized frame, the mass defect is calculated as
 |
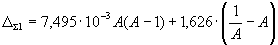(28) |
where ΔΣ1 – a defect of the masses in new rationalized coordinate system, MeV.
It can be seen that semi-empirical dependence (28) is in almost complete agreement with the experimental dependence Δ/А even in the first approximation, except for the range A = 1–20 and the minor deviations at A = 40, 80, 140, 210, and 260. These discrepancies can be explained by the general external unbalance of average quantum characteristics of the nucleus state (spin, parity, analog state) at small A and for magic nuclei. These characteristics are likely to affect the internucleonic interaction.
The deviations from the experimental curve can be removed almost completely by taking into account two last terms of the Weizsäcker formula (the corresponding coefficients should be appropriately recalculated). In this case the Coulomb repulsion forces can be neglected, since they pertain to the interaction different from the mass interaction (mass changes are associated solely with the mass interaction).
Thus, the relationship between the mass defect and the mass number can be written in a final form:
.
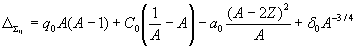Here q0, C0, a0, δ0 are dimensional constants (in amu or MeV).
Close agreement between dependence (28) and the experimental curve allows us to make the following conclusions.
The mass defect originates due to changes in the mass interaction of individual nucleons with the surrounding compositional medium when these nucleons are grouped in a nucleus.
The nuclear saturation property (boundedness of the number of internucleonic interactions) is called into question. The effect of the saturation property and Coulomb forces is replaced by the introduction of the spatial interaction.
The results obtained here can be used in the development of more sophisticated nuclear models.