3.1.2. Связь, информация и исследование потенциала их качественного аспекта

Бритченко И.Г., Бритченко Г.И.

Системы коммуникаций включают связь как важнейшую составную часть, которой отводится относительно большая роль, чем другим ее компонентам. В общем случае под связью понимается то, что объединяет элементы системы в целое. Можно считать, что связь между элементами имеется, если они накладывают взаимные ограничения на поведение друг друга. Отсутствие таких ограничений исключает какие бы то ни было связи. Связи между элементами определяют их организацию, структуру, поведение в рамках целостной системы. Организация системы как свойство, характеризующее взаимозависимое поведение ее элементов, проявляется в ограничении их поведения.

Объединению независимых элементов присуще разнообразие, равное сумме их индивидуальных показателей. Если элементы взаимосвязаны, что проявляется в обоюдном или хотя бы в одностороннем ограничении их поведения, то они менее разнообразны, чем вне зависимости. Величина, на которую уменьшается это разнообразие, выступает количественной характеристикой самой связи и соответствующей ее организованности. Эти связи бывают централизованные (вертикальные), нецентрализованные (горизонтальные), синергические (усиливающие), рекурсивные. Последние представляют собой необратимые связи между экономическими объектами, явлениями, при которых ясно, где причина, где следствие. Например, рекурсивная связь существует между затратами, выступающими в качестве причины, и их результатом как следствием. Особый интерес представляет связь прямая и обратная.

Прямая связь возникает при таком соединении элементов системы, когда выходное воздействие одного элемента передается на вход какого-либо другого. Если все связи прямые, то сигнал, поступающий на вход элемента, не зависит от выходного сигнала этого элемента и системы в целом. При прямой связи информация, поступающая в управляющее устройство, не содержит сведения о состоянии управляемого объекта, а если содержит, то ее называют обратной. При таком соединении элементов связь между выходом и входом того же самого элемента осуществляется непосредственно или через другие элементы системы. Принцип обратной связи универсален, он лежит в основе функционирования автоматических регулируемых систем. Обратная связь независима в коммуникативных процессах, регулирующих поведение системы. Она позволяет передавать информацию об изменении процесса для управления им. Таким образом, в системах с обратной связью выходной параметр отражает свои собственные изменения. Обратная связь существует на определенном участке прямой связи, воздействуя на канал того же или предшествующего участка.

Обратная связь может быть положительной и отрицательной. Положительная способствует развитию системы (движению системы) в том же направлении, отрицательная – препятствует (вплоть до перевода системы в другое направление).

В системе управления увеличение положительной обратной связи α_пол ведет к уменьшению абсолютной величины отрицательной обратной связи α_отр, и наоборот, то есть, если α_пол увеличивается от 0 до +1, то α_отр в то же время изменяется от –1 до 0.

Полная обратная связь α_полная может быть записана как

α_полная = α_пол + α_отр = α_пол + (1 – α_пол) = 1.

Как видно, полная величина обратной связи всегда равна единице.

Система управления может находиться в трех состояниях. При первом состоянии (α_отр = -1; α_пол = 0) энтропия системы равна нулю:

Н = – (0×log₂0 + 1×log₂1) = 0.

Система характеризуется определенностью. Во втором состоянии (α_пол = +1; α_отр = 0) наблюдается то же самое:

Н = – (1×log₂1 + 0×log₂0) = 0.

В третьем же состоянии (α_пол = 0,5; α_отр = 0,5) система характеризуется неопределенностью:

Н = – (0.5×log₂0.5 + 0.5×log₂0.5) = 1.

Проблема принятия решения в этих условиях (условиях неопределенности) нуждается в разработке соответствующих методов и средств выработки информации, так как обратная связь может способствовать и положительному и отрицательному развитию системы, что проявляется в характере самой связи системы как целого с составляющими ее элементами.

На практике, например, при управлении кооперацией труда особое значение придается отношениям между отдельным работником и коллективом. Связи между членами бригады, отдела аккумулируются в общие для всех интересы и направлены в основном на достижение определенных конечных результатов своей деятельности. Эти связи рассматриваются как внутренние. Связи бригады (отдела) с руководителем или другими структурными подразделениями являются внешними.

В теории коммуникации наряду с общими закономерностями формирования этих типов связи изучаются специфические закономерности, которые отражают отношения конечных результатов труда отдельных работников и коллектива. Результаты деятельности бригады (отдела) могут иметь существенное значение не только для предприятия, но и для отрасли, региона, народного хозяйства страны. Теория коммуникации включает в предмет своего изучения проблему связи между субъектом и объектом управления, учитывающую экономические, социальные, психологические и другие аспекты информации и системы управления в целом.

Рассмотренные виды связей по природе своей информационные. А какова же природа самой информации? Из существующих концепций информации, направленных на познание окружающего мира, на наш взгляд, верны те из них, которые строятся на концепции об отражательном свойстве материи. Поэтому информацию будем трактовать как отражение, знания, используемые человеком в своей практической деятельности.

Анализ литературы и практики позволил определить следующие основные свойства информации.

1. Целенаправленность. Передаваемая информация имеет различные цели в зависимости от вида деятельности работников. Основные цели сводятся к информированию, оценке, планированию, контролю, поиску и т. д. Если информация не имеет определенной цели, то она просто является данными.

2. Адресность. Она дополняет характеристику цели. Определенное время информация может находиться без адресата. Без наличия потребителя об информации говорить о ней бессмысленно.

3. Ценность. Единого критерия ценности информации нет и быть не может, так как невозможно найти единую единицу ее измерения, которая однозначно устанавливала бы все возможные варианты определения полученных данных. Однако возможны частные критерии (например, материальный ущерб от неполучения информации), которые будут определяться конкретными задачами.

Отмечают свойства информации, связанные с воздействием на ту или иную систему двух и более сообщений совместно, – неаддитивности, некоммуникативности, неассоциативности.

Неаддитивность информации состоит в том, что результат совместного воздействия на систему двух сообщений не равен сумме результатов воздействия этих сообщений на ту же систему.

Некоммуникативность информации заключается в том, что результат воздействия последовательно во времени на какую-либо систему сообщений А, В, С,Д и т.д. будет отличаться от результатов воздействия на ту же систему тех же сообщений А, В, С, Д и т.д., но следующих друг за другом во времени в другой последовательности.

Неассоциативность информации заключается в том, что результат воздействия последовательно во времени на какую-либо систему сообщений А, В, и С будет отличаться от результата воздействия на ту же систему сообщений А и Д, где Д – информация, полученная в результате совместного действия сообщений В и С.

Свойство концентрации информации во времени и в пространстве основывается на концепции интегрированных систем обработки данных, которые предполагают объединение подавляющего числа экономических данных объектов в информационно-вычислительных центрах, организацию и ведению централизованного нормативно-справочного хозяйства на машинных носителях или в памяти ЭВМ.

Свойства полноты (достаточности), необходимости и избыточности характеризует степень отображения описываемого объекта в используемом для принятия решений сообщения. Полнота (достаточность) информации означает, что сведения об управляемом объекте должны охватить все состояние объекта по всем управляемым параметрам. Добавление любых других сведений не дает в этом случае новых знаний об объекте. Информация считается полной, если на ее основе возможно принятие правильного решения.

Необходимость информации заключается в том, что сведения об объекте должны давать только необходимые знания. Сокращение информации, содержащееся в сообщении, уменьшает в этом случае знания об объекте, но и избыточность сообщения допускается только со специальными целями (как «прочность»).

Точность информации, необходимая и достаточная, – количественная характеристика параметров, описывающих состояние управляемого объекта. Уменьшение их недопустимо, а увеличение – излишне.

Надежность (достоверность) информации, необходимая и достаточная, означает, что имеется полная степень уверенности в неискаженности получаемых сведений.

Своевременность и регулярность. Своевременность информации характеризуется выдержкой интервалов времени, в течение которых поступают необходимые сведения. Задержка информации нарушает режим управления и делает сведения бесполезными. Если сведения об управляемом объекте поступают с требуемой периодичностью, обусловленной режимом управления, то этим самым выдерживается требование регулярности информации.

Старение. Старение информации, т.е. потеря ее ценности с течением времени, означает, что поступившая новая информация изменяет предыдущую. Под новизной информации понимается характеристика ее, влияющая на взаимодействие управляющей системы и управляемого объекта. Новизна сообщения отражает изменения количества информации, необходимого для управления системой. При этом часть существующей информации устаревает.

Пригодность – синтетическое свойство информации, включающее характеристики ценности, полноты (достаточности), необходимости и избыточности, точности, надежности (достоверности), своевременности и регулярности, полезности.

Циркулирующая в управлении производством информация – социальная информация, т.е. знания о производственных отношениях и процессах, отраженных в содержании, структуре, связях и способе принятия решений. Эти знания и дают возможность изменять и улучшать процессы и отношения людей как субъектов и объектов управления, формирующих и использующих социальную информацию.

«Горизонтальные» связи, а следовательно, и информация могут замыкаться не внутри, а через вышестоящие уровни. Это значит, что большая часть данных может быть «отсечена». Недостаточное использование прямых связей на одной ступени иерархии приводит к замыканию «горизонтальных» связей на более высоком уровне, к увеличению информационных потоков. Чтобы избежать этого, необходимо предоставить больше прав низшим уровням управления.

Эффективное использование информации в управлении в значительной мере предопределяется принятой системой ее классификации. Предлагаемая классификация информации по организационным признакам позволяет выделить ее существенные характеристики.

Социальная информация представляет собой единство свободной и связанной информации. Свободная информация актуально существует в работе, в пространстве и во времени, во взаимодействии, обеспечивающем связи между управляющей и управляемой подсистемами, и обладает пространственно-временной структурой. Свободная (рабочая) информация образует входящие и исходящие потоки. Под входящим потоком понимается информация, нуждающаяся в преобразовании и которая затем формирует исходящие потоки, оседает в подразделениях, образуя массивы. Связанная (потенциальная) информация характеризует упорядоченность предприятия как кибернетической системы.

Оперативная информация на объекте управления под воздействием описывающей информации преобразуется в информацию управляющую, которая является продуктом процесса принятия решения. В результате распределения оперативной и управляющей информации рождаются ее потоки. Описывающая информация является составной частью связанной.

Полная информация складывается из потоков и массивов, взаимодействующих между собой и переходящих в свою противоположность.

Немаловажное значение имеет классификация информации по назначению – целеобразующая, мотивационная, справочная и комбинированная. Исходя из сущности процесса принятия решения, на базе переработки и оценки описывающей и оперативной информации, то есть на основе набора альтернатив и доводов, производится принятие решения – инструктивная информация (что и как делать), которая основывается и вытекает из мотивационной (почему, зачем).

При этом следует обратить внимание на адресность информации, как ее важнейшее свойство, так как она находит потребителя, для которого предназначена, а вне адресата – теряет свою полезность.

При классификации информации по отношению к целевой функции – о целях данной системы и о средствах достижения их с последующей разбивкой подмножеств на непосредственные и отдаленные цели и средства – существенным является создание системы, так как иногда то, что является целью данной системы, может быть средством для другой системы.

Классификация информации по назначению и отношению к целевой функции необходима для разработки логических проблем управления и моделей информационных процессов функционирующих объектов. При рационализации информационных потоков выделение необходимых сообщений позволит уяснить, являются ли воздействия непосредственными или отдаленными.

Информацию по отношению к управляющей системе делят на входную и внутреннюю. Классификация информации по типу связи включает подмножества номинальной, порядковой и количественной шкал. Номинальная шкала позволяет различать объекты, идентифицировать их; порядковая – установить соотношение между объектами по определенному признаку, распределив их по уровням, степеням важности и т.п.; количественная же – количественное соотношение между объектами.

Информация бывает первичной, не преобразованной и преобразованной – внутренней и выходной. Преобразованная информация характеризуется типом процедур, степенью и параметрами изменений.

Информацию делят на группы степеней: нулевую (основную, которой соответствует статистическое понятие признака), первую (группированную, отвечающую статистическому понятию показателя), вторую (характеризующую понятие статистической совокупности).

При делении основной информации теряется передаваемый смысл. Сгруппированная информация – определенная последовательность основных данных, характеризующихся своей однозначностью.

Временная классификация одна из важнейших. Она отражает протекание информационных процессов во времени, что является главным условием принятия оптимальных решений. В зависимости от подхода к временному признаку информация рассматривается с разных сторон: по обычной интервальной шкале (периодическая и непериодическая), по сопоставлению времени цикла управления с интервалом между сообщениями (условно – постоянная и условно-переменная), по относительному времени события, связанному с разграничением сообщений (начальных, промежуточных, конечных), и по относительному времени протекания процесса.

Сообщения с длиной интервала более года называются долгосрочными, от года до месяца – текущими, от месяца до смены – оперативными; в рамках смены условно считают сообщениями в реальном времени. Это является основанием для деления информации на условно-переменную и условно-постоянную. Так, в системе оперативного управления предприятием нормативы затрат труда и материалов условно-постоянные, а сообщения о фактических затратах – условно-переменные.

Классификации информации по времени в анализе и проектировании информационных систем, при решении вопросов обработки и передачи информации имеет особое значение. По стадиям процесса управления всю информацию можно разбить на шесть групп: нормативную, плановую, учетную, отчетно-аналитическую, коррекцию нормативных данных, связанную с возмещением затрат.

По структуре информация подразделяется на объективную (субъект и объект), признаковую (время и место, источник и направление, номер документа, порядковые номера строк и граф и т.д.), качественную и количественную (объем, плотность потока, емкость и т.д.).

Данная классификация видов социальной информации основана на требованиях делимости ее по классификационным признакам и объединения подмножеств в делимое множество (при этом исключается пересечение подмножеств). При создании классификации видов информации учтены рекомендации естественности классификации, то есть выбора существенного признака в качестве основания деления и упорядочения элементов внутри подмножеств.

Система информации является производной системы управления. Поэтому непрерывное совершенствование методов управления, структуры и организации функционирования преводит к постоянным изменениям состава, объектов, направлений потоков информации и режимов их передачи.

Анализ литературы и практики позволяет вскрыть резервы оптимизации ситемы организационной коммуникации:

ликвидацию дублирующих потоков и параллельного учета;

четкое определение иерархического уровня, которого должны достигать разного рода сведения;

упразднение излишне дробных функционапльных подразделений; определение необходимого состава и количества показателей в соответствии с параметрами управления стадий процесса;

распределение показателей по уровням управаляющей системы в зависимости от выполняемых задач и функций управления, а также допустимой продолжительности цикла управления;

устранение дублирования показателей в различных потоках информации;

введение информации, свидетельствующей об отклонениях факта от плана (нормы);

увязка периодически документов со сроками регулирования соответствующих процессов;

создание накопительных документов взамен разовых, унификацию форм документов и использование типовых текстов;

установление системы ответственности, позволяющей снизить количество согласований документов;

использование современных способов ведения делопроизводства (регистрация, учет и контроль, справочная работа, курьерская связь и т.п.);

эффективное использование комплексов средств техники управления (обработки, хранения и передачи информации);

разработка рациональной системы организации и др.

Система коммуникации должна выдавать соответствующим руководителям только четкую информацию, которая выходит за рамки саморегулирующейся системы управления и требует определенных действий со стороны руководителей.

Трудоемкость информационных процессов зависит от обработки и оформления документов, что выступает главным экономическим критерием оптимизации системы коммуникации. Трудоемкость обработки – основной показатель эффективности управленческого труда и критерий направления механизации и автоматизации наиболее трудоемких операций.

Методология выбора критериев и направлений совершенствования систем коммуникаций в управлении должна основываться на показателе повышения производительности труда. Его уровень обуславливается совокупностью экономических факторов, количеством и качеством труда, степенью использования средств техники управления, организацией управленческого процесса, сокращением численности работающих и т.д. Поэтому важным является исследование всей совокупности компонентов системы коммуникации.

Между понятиями система и информация существует связь. И систему, и информацию рассматривают как меру потенциальной упорядоченности, сложности и т.д. Поскольку информация отражает общие свойства систем различной природы, она является основой системных исследований. Понятие информации применяется при построении общей теории систем. Поэтому мы рассматриваем информацию как условие потенциала системного исследования.

То, что процессы сбора, передачи, хранения и эффективного использования информации стали предметом специального изучения, объясняется острой социальной потребностью в автоматизации процессов управления. При этом прежде всего возникла необходимость определения способа измерения информации, т.е. на первый план выдвигается количественный подход.

Современная теория информации создавалась на основе развития средств связи – телеграфа, телефона, радио,телевидения и т.д. Решение проблем надежности информационного канала и скорости передачи информации по заданному каналу связи (его пропускной способности) требовало количественного анализа процесса передачи информации. Таким образом, теория информации формировалась по мере решения определенных технических задач, создания эффективных методов передачи информации. При этом допускалось абстрагирование материаьной формы и конструктивных особенностей канала передачи информации. Постановка проблемы в общем виде позволила перейти к математической форме, обладающей еще большей степенью общности и более широкой областью применения теории информации.

Попытки применения теории информации в экономических исследованиях показали необходимость изучения ее качественного аспекта.

Гегель в «Науке логики», анализируя основные категории человеческого мышления, указал на их естественную последовательность: анализ бытия, представляющего собой внешность вещей и явлений, начинается с качественного определения, переходит затем в количественный анализ и заканчивается единством качества и количества, т.е. качественным количеством.

Переход от качественной к количественной стороне понятия всегда сопровождается некоторым его обеднением. Никакая количественная теория не может охватить все аспекты качественного представления, проявлений его потенциала. Вот почему исследование в любой области познания начинается с анализа качественной определенности данной области. Оно представляет собой, с одной стороны, обобщение исторического развития определенного научного знания, а с другой – следствие логического анализа основных этапов этого процесса. Прослеживая формирование теории информации и ее качественного аспекта, целесообразно рассмотреть каждый из них.

Историческая справка становления теории информации такова. Теория информации как наука развивалась своеобразно. В становлении ее большую роль сыграли труды американских ученых К.Шеннона, Н.Винера и всемирно известного русского физиолога И.П.Павлова, который еще в 1930-е годы вплотную подошел к сравнению мозга с электрическими переключательными системами. Уже около ста лет, начиная с работ Дж.Максвелла и И.А.Вышнеградского, учеными разрабатывается теория регулирования систем с обратной связью.

В начале 20 века в Екатеринославе Я.И.Грдина опубликовал работы по динамике живых организмов, в которых рассматривались динамические системы «с волевыми связями». Перечень ученых, которые внесли определенный вклад в формирование теории информации, можно продолжить. Сам Н.Винер, например, ссылается на работы русских ученых – А.Н.Крылова, Н.Н.Боголюбова, Н.Н.Колмогорова и П.А.Козуляева. В.И.Шестаков независимо от К.Шеннона открыл применимость математической логики Дж.Буля для исследования переключательных схем. Заслуживает внимания работа А.А.Богданова «Всеобщая организационная наука (тектология)». Ее автор во многом был предшественником Н.Винера, по крайней мере, в системной части кибернетики.

Используя в своих работах понятия «передача информации», «канал информации», «количество информации», эти и другие авторы способствовали тем самым созданию фундамента новой теории. Известная работа К.Шеннона, которую принято считать основополагающей в развитии теории информации, называлась «Математическая теория связи». Это наименование точно отражало ее содержание. Заслугой К.Шеннона следует считать то обстоятельство, что он рассмотрел основные проблемы техники связи, сведя их в единую строгую систему математических построений и выводов.

Так как теория информации разрабатывалась главным образом на основе теории техники связи, которая игнорировала содержание передаваемой информации, сам термин «информация» и понятия, связанные с процессами информирования, долгое время не были определены.

Впревые понятие «количество информации» появилось в работах Р.Фишера (1921 г.) по вопросам математической статистики. В результате количество информации в передаваемом по каналу связи сообщении стали определять, пользуясь формулой ( ( ((, где К – количество передаваемой информации; В – ширина полосы частот сигналов,используемой для передачи; Т – продолжительность передачи сообщения, преобразованного в сигналы.

Американский инженер Хартли вводит еще один аргумент, влияющий на количество информации в передаваемом сообщении:

I = 2ВТlog₂S, где I – количество переданной информации; S – число поддающихся различению ступеней амплитуды сигнала.

С 1928 г. известна формула Хартли, в которой в качестве практической меры информации был принят логарифм возможных последовательностей символов:

Н = nlog₂S или Н = log₂Sⁿ, где Н – количество информации; n –число выборов; S – число первичных символов, возможных при каждом выборе; Sⁿ – число различных последовательностей символов.

Наконец, в 1948 г. К.Шеннон вывел формулу, ставшую основой количественной теории информации:

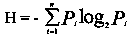
Она выражает энтропию множества n вероятностей P₁, P₂, … P_n, и в числовом виде описывает «количество информации» (возможность выбора, неопределенность).

Формула применяется также в следующем виде:

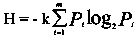
где m – число символов (элементов), из которых может быть составлено сообщение; k – число символов в одном сообщении; P_i – вероятность появления i-го элемента в сообщении.

Из формулы следует, что Н=0 только тогда, когда одна из вероятностей равна единице (т.е. все остальные вероятности равны нулю). Это есть состояние определенности, или уверенности.

Таким образом, утверждение, что из множества событий, каждое из которых потенциально может наступить с определенной вероятностью, одно действительно наступает и сводит неопределенность к нулю, позволяет, по словам Шеннона, рассматривать величину как разумную количественную меру возможности выбора, т.е. меру количества информации.

Когда все вероятности равны между собой (Р = 1/n), величина Н принимает максимальное значение: Н = log₂n.

На основании этой формулы за единицу информации было принято такое ее количество, которое соответствует утверждению, что произошло одно из двух равновероятностных событий. В соответствии с выведенной еще раньше Хартли: Н = log₂n.

Таким образом, понятие «количество информации» складывалось путем разумного терминологического соглашения, основанного на математической формуле. Однако само по себе оно объясняет только количественный аспект. Согласно классической концепции информации последняя рассматривается как вероятность поступления сигнала в канале связи, мера устранения неопределенности знания у получателя сигнала (сообщения) о состоянии передатчика или о некотором событии.

Информация и неопределенность. С ростом знаний всегда уменьшается неопределенность тех или иных потенциальных событий в изучаемой области. Неопределенность, с количественной точки зрения, легко выражается вероятностью. Чем меньше вероятность того или иного потенциального события, тем больше его неопределенность. Именно изменение неопределенности в связи с изменением знаний и описывает количественная теория информации.

Определенность – понятие противоположное неопределенности. Возрастание неопределенности означает уменьшение определенности и наоборот. Понятия определенность и неопределенность легко переводятся в понятия упорядоченность и неупорядоченность. К.Шеннон считал, что информация, связь, в процессе которой устраняется неопределенность, а Н.Винер отождествлял ее с мерой упорядоченности.

Специфика того или иного явления выражается не одним каким-либо свойством, а их набором. Качественная сторона явления состоит не только в совокупности этих свойств, но и в наличии определенной потенциальной функциональной связи между ними. Изучая свойства явлений, мы расширяем область познаваемых объектов – предметов и явлений действительности, обладающих чертами потенциала неопределенности, упорядоченности и неупорядоченности. Это означает, что предметом количественной теории информации могут быть любая вещь, явление, событие, обладающие свойствами, аналогичными соответствующему свойству информации как знания. При таком подходе очевидным становятся односторонность количественной теории и принципиальная неограниченность области ее применения.

Определенность и неопределенность, упорядоченность и неупорядоченность – свойства, присущие познанию так же, как и любому потенциально существующему явлению действительности. Однако из этого общего положения еще нельзя сделать вывод о безусловной применимости теории информации ко всем вещам и явлениям. Для окончательного решения вопроса необходима соответствующая идеализация рассматриваемого явления. Сущность этой процедуры заключается в придании реальным объектам такой потенциально мысленной формы, которая бы не исключала возможности применения теории информации в данной области познания.

Теоремы К.Шеннона описывают некоторую идеализированную ситуацию. К реальным процессам они применимы в той мере, в какой эти явления приближены к идеализированным условиям. Именно благодаря идеализации можно рассматривать любую потенциальную последовательность знаков как несущую информацию, независимо от того, заключен в ней какой-нибудь реальный смысл или нет. Всякий процесс передачи информации в большей или меньшей степени можно приблизить к идеализированной ситуации, т.е. чем дольше идет передача по данному каналу, тем более он приближен к идеализированному каналу теории информации.

В реальном акте передачи информации смысловая ее сторона существенна лишь в том случае, если информацию получает человек. Если же информацию в конечном счете использует машина, смысловая ее сторона не влияет на последовательность знаков сообщения.

Процесс познания сводится к тому, что на основе некоторой потенциальной качественной неопределенности проводится количественный анализ. Результат последнего – некоторые качественные аспекты познания, определяемые самой количественной теорией. Таким образом, неопределенность рассматривается как потенциальный качественный аспект количественной теории информации.

Информация как выбор. Присущий процессу познания отбор (выбор) подходящих вариантов из некоторого их потенциального множества на протяжении долгого времени развития теории информации показал, что понятие потенциального выбора играет существенную роль в любой стадии процесса познания и особенно на ступени абстрактного мышления. Сам математический аппарат теории информации, по существу, подсказывает именно этот вывод.

В работе электронно-вычислительной машины потенциальный выбор представляет собой основной метод переработки информации. Обобщая практику работы вычислительной техники, можно сказать, что сущность процесса переработки состоит именно в выборе подходящих потенциальных вариантов. Поэтому для процесса мышления с участием ЭВМ необьходимы некоторый источник случайных событий и система, способная осуществлять выбор из этого потенциального множества событий.

Определение информации через выбор содержалось, между прочим, в той форме количественной оценки информации, которую предложил Хартли. Если мы имеем некоторую задачу, то можно ставить вопрос об априорно возможных ее решениях. Если при этом все они равновероятны, то мы получим тот случай, для которого Хартли предложил свою меру количества информации. Пусть задача имеет N – какое-то число вероятных решений. Тогда I = log₂N, где I – количество информации, а N – число априорно равновозможных исходов. Это означает, что сообщение, дающее нам возможность выбрать один из N случаев, имеющихся априорно для сообщения, несет информацию, пропорциональную логарифму числа исходных потенциальных вариантов.

Ясно, что проблема выбора связана здесь непосредственно с проблемой неопределенности. Информация рассматривается с точки зрения возможности устранить потенциальную неопределенность. А единицей информации уславливаются считать то ее количество в сообщении, которое сокращает наше неведение ровно вдвое.

Многократное повторение выбора нуждается в получении многих единиц информапции. В результате I единиц информации сужают область выбора в 2 раза. Нетрудно понять, что если сообщение указывает на единственный вариант из равноправных 64-х, то оно несет шесть единиц информации, из 128 – семь и т.д. Во всех этих случаях количество информации равно степени, в которую нужно возвести двойку, чтобы получить число равноправных вариантов выбора.

Итак, если сообщение указывает на один из N равноправных вариантов, то оно несет количество информации, равное log₂N. (Единица информации получила название «бит». За ним кроется сокращение английских слов binary digit – двоичная единица). Если рассматривать зависимость количества информации от числа вариантов выбора, то окажется, что количество информации равстет далеко не так быстро, как число вариантов выбора. Если широта выбора увеличивается в геометрической прогрессии, то информация – в арифметической. Это свойство информации трудно воспринять со всей четкостью, но оно проявляется во многих случаях, когда ведется отыскание нужного потенциального варианта среди массы подозреваемых. Несколько лишних бит иногда приводит к окончательной разгадке сложной задачи.

Ситуация, когда число априорно возможных решений конечно и все они равновероятны, для теории информации является элементарной. В общем случае, когда вероятность каких-либо исходов различна, для выбора используют формулу Шеннона. Согласно этой формуле исходная энтропия

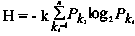
где P_ki – вероятность отдельного исхода решаемой задачи. Сумма P_ki равна единице.

Если обозначить априорно возможные исходы через a₁, a₂, … a_n, то им будут соответствовать вероятности P₁, P, … P_n.

Нетрудно заметить, что формула Шеннона переходит в формулу Хартли при P₁ = P₂ = … = P_n.

Таким образом, процесс выбора, который так очевиден в формуле Хартли, описывается формулой Шеннона. Разница только в том, что формула Шеннона предполагает более конкретную ситуацию, чем формула Хартли.

Представление об информации как о потенциальном выборе дает возможность показать объективный качественный смысл применения логарифмов при оценке количества информации. Если информация связана с процессом выбора определенного события из некоторого множества, то можно поставить вопрос о его способе. Простейшим из них является последовательный перебор всех потенциальных событий. При таком подходе естественно рассматривать информацию как величину, прямо пропорциональную числу событий. Если выбор осуществляется путем деления множества событий на части, то число операций будет пропорционально логарифму этого числа. В качестве основания можно взять число, которое указывает, каким образом производилось деление множества. Таким образом, логарифм в формуле, определяющей количество информации, характеризует метод определения самого количества.

Естественно задать вопрос: как обстоит дело в реальных системах, перерабатывающих информацию; какой потенциальный метод выбора применяется в них? Ответ на этот вопрос является очень важным для конструирования соответствующих устройств. В психологии имеется экспериментальный материал, позволяющий утверждать, что, повидимому, именно подход последовательного деления, разбиения множества применяется нервной системой при переработке в ней информации.

Информация как характеристика сложности. Третьим аспектом качества информации выступает ее свойство быть характеристикой потенциала сложности любой системы. Если первые два свойства – определенность и неопределенность тех или иных событий, а также сам процесс потенциального выбора более или менее непосредственно содержатся в качественной характеристике знания и познания, то о потенциальной сложности как свойстве систем этого сказать нельзя. Мысль об информации как о выражении степени потенциальной сложности возникает прежде всего постольку, поскольку речь идет о материальных структурах, построенных из некоторых элементов.

На первый взгляд естественно оценивать сложность той или иной системы по числу элементов в ней. Но опыт исследований в самых различных областях науки свидетельствует, что в действительности необходимо учитывать не только элементы, но и потенциально возможные между ними связи. Эти связи постоянно изменяются и, следовательно, переводят систему в разнообразные состояния. Подсчитано, что при семи элементах (рабочая сила, оборудование, материал, энергия и др.), связь между которыми либо есть, либо отсутствует, система может иметь 2⁴² состояния.

Французский консультант по вопросам управления Грейкунас разработал математическую формулу, описывающую экспоненциальный рост сложности связи при увеличении числа подчиненных. Если р – число подчиненных, то количество взаимосвязей всех видов определяется из зависимости .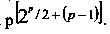

Между совокупностью элементов и формой их не может быть однозначной зависимости. Содержание (элементы) определяют не конкретную форму связи, а множество потенциально возможных систем.

Рассмотрим случай, когда имеется конечное число различных элементов. Если не дано больше никаких конкретных свойств, то можно считать, что в данном множестве потенциально возможны между элементами все связи. Это самое слабое из всех ограничений, которые могут быть наложены на систему в целом. Для такого случая допустимы все мыслимые (абстрактно возможные) потенциальные структуры. Единственное ограничение – число самих элементов. Тогда количество возможных систем будет максимальным и все они окажутся равноправными и равновероятными.

Применяя формулу количества информации, получим, что реальная система, оценивая по отношению к указанным предположениям, несет информацию I = log₂N, где N=f(n). Количество информации определяется через log₂N. Здесь N – число возможных систем из n элементов и поэтому является функцией n.

Понятие множества само по себе не приписывает элементам никаких свойств, кроме потенциальной способности отличаться друг от друга. В действительности же элементы могут различаться лишь постольку, поскольку они обладают какими-либо свойствами. Способность процессов, свойств, отношений отличаться от остальных, быть чем-то особенным, своеобразным – это не что иное, как отрицательное выражение определенности процесса, свойства, отношения, т.е. качества. Таким образом, понятие множества логически выводится из понятия качества и представляет собой своего рода переход от общефилософского понятия к конкретно математическим представлениям.

Информация как разнообразие. Рассматривая понятие информации и те качественные потенциальные аспекты, которые связаны с ее количественной теорией, мы по сути исходим из идей Шеннона, развитых им в процессе анализа проблем, возникающих при передаче информации по каналам связи. Однако такой подход содержит в себе элементы субъективности. (Например, при определении количества информации основой служит учет априорной вероятности событий). По нашему мнению, определение вероятности тех или иных потенциальных событий в значительной мере зависит от уровня знаний. Поэтому следует рассматривать определение априорной вероятности как функцию уровня нашего знания об объекте.

В теории Шеннона процесс передачи информации принят бесконечным, что позволяет исключить индивидуальные особенности ее получателя. Чтобы уровнять всех возможных получателей, конкретный получатель информации, обладающий определенными знаниямии способностью предвидеть априорную вероятность события, заменяется типичным получателем сообщений со средними способностями определенния априорной вероятности событий. Такой усредненный получатель информации должен обладать соответственным уровнем знаний. Это заставило искать новые пути интерпретации теории информации. В часности, необходимо было освободить понятие информации от момента субъективности.

Так, У.Р.Эшби определил информацию через понятие «разнообразие». В данном случае количество информации можно рассматривать как меру потенциального разнообразия. Эшби отмечает, что такой подход позволяет использовать разные методы определения количества информации как количества потенциального разнообразия – в частности, рассматривать разнообразие как количество различных элементов. Однако на наш взгляд более общим и удобным является теоретико-множественный способ логарифмического выражения количества разнообразия. статистический подход к передаче информации как к процессу легко может быть переведен в эту форму. Всякая передача информации представляет собой последовательность состояния передатчика и приемника, которую можно рассматривать как потенциальное множество состояний. Таким образом, понятие теории информации легко переводится на язык теории множеств или на язык разнообразия.

Оценивая информацию как разнообразие, мы тем самым охватываем не только область существующего, но и область возможного, так как, оценивая количество информации или количество разнообразия, можно учесть реально существующее разнообразие. Тогда количество информации как количество разнообразия, во-первых, будет выражаться логарифмом числа различных элементов данной области, взятым по некоторому основанию. Во-вторых, в качестве элементов множества можно рассматривать и область возможного. Тогда количество информации как количество разнообразия будет представлено логарифмом числа потенциально возможных элементов (или состояний).

Само по себе разнообразие не является собственно свойством вещей, а зависит от подхода к ним. В одной и той же области можно обнаружить разнообразие. Так, например, организм можно рассматривать как множество органов, из которых он состоит. Однако тот же организм можно разложить на множество клеток, и тогда количество разнообразия в нем значительно возрастет. Данный процесс можно продолжать, переходя ко все более тонким уровням организации. Не вызывает сомнения тот факт, что в одном и том же явлении можно по-разному оценивать количество разнообразия.

Каждый объект действительно обладает разными уровнями организации, и количество разнообразия меняется от уровня к уровню. Каждый уровень организации имеет свое количество информации как количество разнообразия. То обстоятельство, что сам объект во всех отношениях обладает неодинаковым количеством разнообразия, дает возможность в зависимости от целей получать какое-то количество разнообразия. Эта точка зрения позволяет применять теорию информации при оценке уровня организации потенциально возможных систем. Чем сложнее система, тем больше в ней элементов, образующих некоторое множество или разнообразие.

Если правильно выбрать исходный уровень организации, который служит своеобразной точкой отсчета, то можно показать, как идет накопление информации. С этой точки зрения любой объект – сгусток информации. Такой подход позволяет в терминах разнообразия описывать поведение сложных динамических систем. Если система принимает ряд последовательных состояний, то в силу этого она обнаруживает потенциальное разнообразие состояний, развернутых во времени. При оценке той или иной системы приходится учитывать множество возможных линий поведения. Их совокупность должна исчерпать все множества возможных состояний системы.

Таким образом, анализ разнообразия связан с выяснением отношения реализованного множества состояний ко всему возможному множеству. Все действительные объекты представляют собой ограниченное разнообразие возможных состояний. Через это понятие, т.е. через ограничение разнообразия, можно представлять информацию как определенность вещей и явлений. Всякая вещь представляет собой ограничение разнообразия. Ничем не ограниченное потенциальное разнообразие равно неопределенности.

Информация и энтропия. Мера статистического потенциального разнообразия исходов опыта (практика всегда оставляет место для неопределенности исхода очередного опыта) именуется энтропией. Сообщение об исходе опыта снимает неопределенность, доставляя количество информации, равное уменьшению энтропии. Следовательно, энтропия есть мера недостающей информации о состоянии системы. По знаку она противоположна информации. Поэтому количество информации отождествляется с отрицательной энтропией – негэнтропией.

Энтропия системы тем выше, чем больше в ней степеней свободы. Так, с усилением неопределенности производственной системы (поломки оборудования, брак, невыход на работу) повышается и ее энтропия. В этом плане управление представляет собой антиэнтропийный процесс. Следовательно, чтобы производительная система могла нормально функционировать, нужна достаточная информация о производственных явлениях и способах воздействия на них.

Понятие энтропии используется не только в науке управления. Оно введено в молекулярно-кинетическую теорию статической физики. Основная формула Шеннона – количества энтропии – аналогична формуле Больцмана, но последняя является частным случаем первой. В ней коэффициент перед знаком суммы имеет вполне определенный физический смысл и размеренность, междлу тем как в формуле Шеннона этот коэффициент – абстрактное число, определяемое из условий задачи.

Но Больцман первый предпринял попытку дать содержательное понятие энтропии. Он предложил своеобразную модель, согласно которой любое состояние газа имеет определенную вероятность. Оказалось, что для газа наиболее вероятно состояние хаотического движения молекул. Руководствуясь молекулярно-кинетической теорией, можно рассматривать энтропию как состояние хаотического движения молекул. Такая интерпретация понятия энтропии стала общефизической, а закон ее возростания в изолированной системе рассматривается как тенденция перехода от упорядоченности к беспорядку.

Существует ли аналогичная связь между информационными и энергетеческими процессами? Рассмотрим для этого «Демон Максвелла». Извесный английский физик Д.Максвелл рассуждал следующим образом. Предположим, что сосуд с газом разделен стенкой с дверцей. Дверцей управляет маленькое существо – «демон», обладающее способностью различать быстрые и медленные молекулы газа. Управляя дверцей, «демон» мог бы собрать в одной части сосуда все медленные молекулы, а в другой – все быстрые, т.е. вопреки второму началу термодинамики он оказался бы в состоянии уменьшить энтропию замкнутой системы, которой является сосуд с газом. Если оба отделения сосуда соединить тепловым двигателем, то он будет вырабатывать энергию, т.е. получится вечный двигатель.

Было понятно, что подобный «демон» практически невозможен, однако решить этот парадокс теоретически долгое время не удавалость. Между тем Л.Сциллард в 1929 г. решил его весьма просто. Иллюзия «вечного двигателя» второго рода на примере «демона Максвелла» возникла потому, что игнорировались затраты энергии на получение информации о скорости движения молекул. Дело в том, что для того, чтобы различать быстрые и медленные молекулы, необходим один бит информации, который следует передать «демону». На это нужно потратить минимум именно той энергии, которую может создать машина с «демоном» внутри.

«Демон» не может действовать, не получая информации о скорости движения. А информация представляет собой отрицательную энтропию. Понятие энтропии газа и энтропии как меры неопределенности системы в данном случае совпадают. Изменение же энтропии газа – это внешняя и внутренняя работа, выраженная в каллориях на единицу газа. Таким образом, для получения целостной картины реального мира к четырем известным категориям – материи, движению, пространству и времени – оказалось необходимым добавить понятие информации. Информационные процессы направлены от настоящего к будущему. Их необратимость выражена в характеристике энтропии.

Возрастанию беспорядочности противопоставляются процессы информации, которые вносят порядок в хаос. В этом и проявляется важнейшее потенциальное свойство информационной функции в системе управления.

Отдельно следует подчеркнуть ту мысль, что, если признавать информацию как пятое начало мира, то вправе говорить о коммуникативном аспекте информации. Наше исследование посвящено проблеме коммуникации в системе управления, поэтому в этом плане мы выделяем информационный аспект коммуникации.