Сравнительная характеристика методов выделения локальных аномалий
В.П.Дудкин, И.Н.Кошелев
Рассмотрим различные методы разделения локальных и региональных аномалий на условном теоретическом гримере.
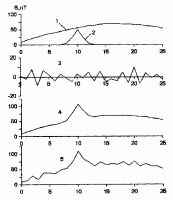
На рис. 3 представлены : график нелинейного регионального магнитного поля, которое изменяется по закону, близкому кривой второго порядка (кривая 1); локальная аномалия (кривая 2), создаваемая сильно разрушенной трипольской площадкой, и фон помех (кривая 3), рассчитанный генерацией случайных чисел в диапазоне от -10 до +10 нТ с нулевым средним и среднеквадратическим отклонением s = ± 5 нТ; сумма региональной и локальной составляющих представлена кривой 4, а суммарное поле, включая помехи – кривой 5.
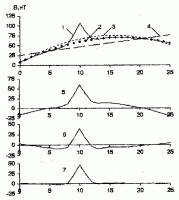
Вначале проведем исследования корреляционным методом. Как видно на рис. 4, региональная компонента, рассчитанная как линейный тренд (кривая 4), существенно отличается от теоретических значений регионального поля. Отклонения достигают ± 20 нТ (см. табл. 1). Погрешность аппроксимации регионального фона нелинейным трендом (кривая 2) гораздо ниже и не превышает ± 2 нТ, т.е. на уровне точности отсчитывания магнитометра.
Существенно отметить, что в процессе расчета коэффициентов тренд-функции методом наименьших квадратов при вычислении промежуточных сумм следует исключать отдельные “выбросы” и аномальные значения наблюденного поля. В качестве критерия “аномальности” можно принять, например, условие выполнения неравенства
| abs(B(i + 1) – B(i)) > G | (14) |
где G – нормальный (допустимый) горизонтальный градиент поля по профилю.
Величина G выбирается на основании анализа исходных данных с учетом характера искомых локальных аномалий на обрабатываемой площади. В данном случае было принято G = 10 нТ/м. Игнорирование условия (14) приводит к необоснованному завышению или занижению (при больших отрицательных аномалиях) уровня регионального поля. Для данного примера это иллюстрируется кривой 6 на рис. 4.
Таблица 1. Отклонение значений регионального поля, рассчитанных корреляционным методом, от теоретических значений.
| Метод расчета | Минимальное отклонение, нТ | Максимальное отклонение, нТ | Стандарт s, нТ |
| Линейный тренд | -14 | +21 | ±10 |
| Нелинейный тренд (без учета аномальных значений поля) | -5 | +10 | ±4.6 |
| Нелинейный тренд (с исключением аномальных значений поля) | -2 | +2 | ±1.4 |
Таким образом, оптимальный подход к выделению регионального поля предусматривает вычисление нелинейного тренда в сочетании с процедурой исключения резко отличающихся значений наблюденного поля. Об этом убедительно свидетельствуют представленные на рис. 4 локальные аномалии, полученные для случаев линейного, нелинейного регионального поля и нелинейного тренда с учетом неравенства (14). На графике локальной аномалии, вычисленной в предположении линейного тренда (кривая 5), отчетливо видна неучтенная криволинейная составляющая регионального поля, обуславливающая резкое отличие выделенной аномалии от истинной (теоретической). График локальной аномалии, рассчитанной для нелинейного регионального фона без исключения аномальных значений поля (кривая 6), осложнен ложными минимумами за счет завышения уровня региональной компоненты магнитного поля. И только в случае расчета нелинейной региональной составляющей с учетом резко отличных аномальных значений поля (кривая 7) получаем практически не искаженную локальную аномалию, максимально близкую теоретической. Количественная характеристика рассмотренных вариантов расчетов приведена в таблице 1.
Сравним теперь результаты расчетов корреляционным методом с другими методами разделения региональных и локальных аномалий.
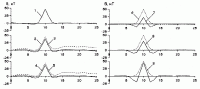
Рис. 5. Пример выделения локальной магнитной аномалии. 1 – корреляционным методом; 2, 3 – пересчетом в верхнее полупространство; 4, 5 – энергетическим фильтром; 6 – теоретическая кривая; 7, 8 – методом усреднения по 5-ти и 7-ми точкам; 9 – вариации по методу Б. Андреева.
На рис. 5 приведены локальные аномалии, вычисленные на основе усреднения наблюденного поля, пересчета в верхнее полупространство и фильтрации энергетическим фильтром.
Как видно из рисунка, вычисленная корреляционным методом локальная аномалия (кривая 1), практически полностью совпадает с теоретической (кривая 6).
Остаточная локальная аномалия, полученная на основе аналитического продолжения магнитного поля в верхнее полупространство (кривая 2), характеризуется систематически завышенными значениями поля. Это объясняется тем, что при пересчете вверх уменьшается амплитуда не только локальных, но и региональных аномалий. Вследствие этого уровень поля, полученного на высоте Н, которое мы принимаем за региональное, в случае его нелинейности всегда будет несколько занижен. Таким образом, остаточное поле фактически является суммой локальной аномалии и неучтенной при пересчете вверх криволинейной части регионального тренда. Этот остаточный тренд легко исключается корреляционным методом. В результате получим локальную аномалию, близкую теоретической (кривая 3 на рис. 5).
Сходная картина наблюдается и в случае выделения локальной аномалии энергетическим фильтром. Криволинейная составляющая регионального поля оказывается не отфильтрованной и наблюдается совместно с локальной аномалией (кривая 4). После исключения остаточного тренда корреляционным методом локальная аномалия принимает нормальный вид (кривая 5). Кроме энергетического фильтра нами испытаны и другие (фильтр Шеппарда, В. Мягкова и др.), которые в наших специфических условиях не обеспечивают сохранение форм, размеров и амплитуды искомых локальных аномалий (см. табл. 2).
Локальные аномалии, вычисленные методом усреднения, представлены на рис. 5 кривыми 7 (усреднение по 5-ти точкам) и 8 (расчетный интервал – 7 точек). Они значительно отличаются от теоретической кривой (6) по ширине и амплитуде и сопровождаются дополнительными ложными минимумами. Вариации магнитного поля по Б. Андрееву (кривая 9), хотя и осложнены дополнительными минимумами, но, по крайней мере, сохраняют амплитуду, близкую теоретической локальной аномалии.
Количественная характеристика различных методов выделения локальных магнитных аномалий приведена в таблице 2.
Из сравнения всех полученных результатов легко установить, что метод выделения локальных аномалий, основанный на тренд-анализе исходных данных, выгодно отличаются от других рассмотренных методов и его можно рекомендовать как лучшее средство разделения локальных и региональных аномалий при обработке материалов магнитометрических съемок археологических объектов.
Приемлемые результаты можно получить также на основе пересчета наблюденного поля в верхнее полупространство или применением энергетического фильтра, однако полученные при этом аномалии будут содержать неучтенную часть региональной составляющей исследуемого поля, которую все равно придется исключать тем же корреляционным (или каким-либо иным) методом.
Недостатком корреляционного метода является то, что в процессе расчета локальных аномалий фильтрации помех не происходит. Поэтому следующая задача обработки состоит в том, чтобы подавить помехи, максимально сохранив полезные аномалии.
Таблица 2. Сравнение результатов выделения локальных аномалий различными методами.
| Преобразование | Уменьшение амплитуды локальной аномалии, А / А теор, % | Уменьшение ширины локальной аномалии, Х / Х теор, % | Относительная амплитуда сопутствующих минимумов, А min /А maх, % |
| Корреляционный метод (исключение нелинейного тренда) | 94 | 0 | на уровне помех |
| Вычисление остаточных аномалий (на основе пересчета вверх) | 72 | - 20 | - 8 |
| Энергетический фильтр | 72 | - 20 | - 8 |
| Вариации по Б. Андрееву | 90 | - 15 | -42 |
| Фильтр Шеппарда | 44 | - 30 | -45 |
| Фильтр В. Мягкова | 58 | - 20 | - 30 |
| Усреднение по 3 точкам | 24 | -40 | - 33 |
| Усреднение по 5 точкам | 46 | - 30 | -39 |
| Усреднение по 7 точкам | 60 | - 20 | - 33 |