Індекси якісних показників
Андрієнко В.Ю.
Функціональним початком будь-якої системи явищ, що індексуються виступає кількісний показник. Однак, з метою більш послідовного викладу розглянемо спочатку питання агрегатного індексування якісних показників, тому що тут статистика нагромадила значні проблеми та протиріччя.
У агрегатному індексуванні якісні показники виступають і як чинник об’ємного показника, і як власне результативний показник, що іменується середньою змінного складу. І в обох випадках наявна система агрегатного індексування наштовхується на непереборні протиріччя, що породжують постійні дискусії.
Якщо якісний показник спільно з кількісним розглядаються як чинники об’ємного показника, виникає проблема їх зважування в агрегатних індексах, яка, незважаючи на існування безлічі різних підходів, остаточно ще не вирішена. Тому практикам надане право користуватися будь-яким з двох можливих систем зважування, що, природно, приводить до неоднозначних висновків, які отримуються при врахуванні впливу різних чинників на об’ємний показник.
Неспівпадіння результатів факторного аналізу пояснюється в цьому випадку непостійністю індексу структурних зрушень, який в залежності від системи зважування приєднується то до кількісного, то до якісного чинника. Це істотна вада агрегатного індексування, яку можна ліквідувати шляхом переходу до ізольованого індексування кількісного і якісного чинників. При такому підході структурний чинник повністю приєднується до якісного чинника, оскільки динаміка останнього відображається індексом змінного складу замість індексу фіксованого складу, який має місце при індексуванні, що склалося. У свою чергу при факторному аналізі середньої змінного складу виникає можливість виокремити структурний чинник як самостійний елемент агрегатних індексів, зумовлюючий безпосередню зміну якісного показника.
Таким видається загальний напрям агрегатного індексування як системи відповідних індексів. Але тут виникають проблеми щодо побудови системи індексів середньої змінного складу.
Основна мета індексування середньої змінного складу – визначити в "чистому" вигляді роль основних чинників, що впливають на її динаміку, якими є, зокрема, зміна рівнів осереднюваної ознаки та структура сукупності, що змінилася. Досягнення цієї мети можливо лише при одній умові – якщо структурний чинник буде мати особливу форму кількісного відображення в статиці. Такою формою є розглянутий нами структурний коефіцієнт К, що дозволяє корінним чином змінити систему індексів середньої змінного складу. Перш ніж перейти до конструювання моделей індексного аналізу якісних показників на основі зазначених вихідних позицій, необхідно визначити практичні цілі і задачі такого аналізу. Це особливо стосується середніх величин, оскільки в рамках індексного методу вони виконують дві ролі. По-перше, індексний аналіз переслідує мету найбільш точно охарактеризувати абсолютний і відносний розвиток рівня якісного явища, що відображається середньою величиною, розуміючи під цим рівнем внутрішню, специфічну властивість даного явища. Наприклад, середня врожайність, будучи біологічною властивістю споріднених сільськогосподарських культур, для певної практичної мети виявляє інтерес саме в цьому відношенні, зокрема з її динаміки можна судити про досягнуті успіхи в селекційній, насінницькій, біологічній та інших сферах діяльності. По-друге, середня величина неодмінно бере участь в певній системі економічних явищ, в зв’язку з цим їй належить істотна роль як елементу системи. Так, врожайність є одним з елементів формування валових зборів зерна. Тому необхідно знати її роль в цьому процесі, а також особливості взаємодії з іншими елементами, зокрема, зі структурним чинником.
Отже, виходячи з загальнометодологічного принципу індексування, який полягає в тому, що результативний показник дорівнює добутку його чинників, будь-яку середню змінного складу у можна представити як похідну від середньої незваженої у і структурного коефіцієнта К :
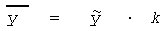
Звідси індекс середньої змінного складу в загальному вигляді описується формулою:
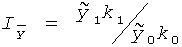
Це і подальші положення підтверджують наступні дані.
| Ячмінь | Овес | Всього | ||||
| Показник | базисний період | звітний період | базисний період | звітний період | базисний період | звітний період |
| Посівна площа, га | 150 | 180 | 50 | 40 | 200 | 220 |
| Врожайність, ц/га | 12,0 | 14,0 | 9,0 | 10,0 | 11,25 | 13,273 |
| Валовий збір, ц | 1800 | 2520 | 450 | 400 | 2250 | 2920 |
Визначимо складові середньої зваженої врожайності.
I. Базисний період:
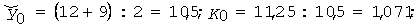
ІІ. Звітний період:
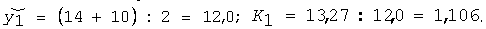
Індекс середньої зваженої врожайності в розгорнутому вигляді складе:
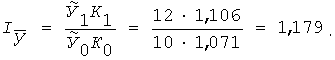
Звідси індекс врожайності фіксованого складу має формулу:
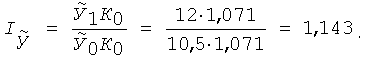
Чисельник цього співвідношення дійсно являє собою той граничний рівень середньої врожайності, який мав би місце при відсутності змін структурного порядку, тобто при незмінності співвідношень між врожайністю окремих культур, а також між посівними площами окремих культур. Тільки при такій умові можна стверджувати, що якісна складова динаміки повністю елімінована від її структурної складової.
До такого результату не може привести традиційний індекс фіксованого складу, зважений по структурі базисного періоду. У цьому переконує його обчислення традиційним способом:
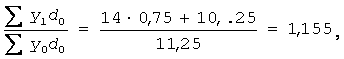
де d0 – питома вага посівних площ культур в базисному періоді.
Наявність відмінностей між індексами фіксованого складу, обчисленими різними способами, пояснюється тим, що традиційна формула не враховує структури (співвідношення) індивідуальних рівнів врожайності, а запропонована формула враховує. Так, врожайність більш продуктивної культури в базисному періоді була вищою в 1,33 рази порівняно з менш продуктивною, а у звітному – в 1,4 рази. Випереджаюче зростання врожайності більш продуктивної культури, якій до того ж належить переважаюча питома вага в посівах, виявилося позитивною зміною по відношенню до середньої зваженої врожайності звітного періоду, що і знайшло відображення в традиційній формулі розрахунку. Але це результат зміни не власне якісного чинника, а його структури, що в поєднанні зі структурою кількісного чинника дало певний економічний ефект. Іншими словами, в традиційній формулі має місце змішування власне якісного та структурного чинників.
Індекс повних структурних зрушень при повному абстрагуванні від індивідуальних рівнів врожайності складе:
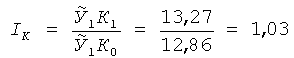
Він включає сумарний результат взаємодії структури посівних площ зі зміною співвідношень між індивідуальною врожайністю. Тому даний індекс відображає, по-перше, всі структурні зміни, по-друге, повністю елімінований вплив структурного чинника від якісного. Крім того, будучи сумарним, він дозволяє виділити вплив, пов’язаний зі зміною співвідношень між індивідуальною врожайністю, з одного боку, і пов’язаний із зміною структури посівних площ, з іншого.
Структурний чинник, пов’язаний зі зміною співвідношень між індивідуальними значеннями врожайності при незмінній структурі посівів, можна визначити за формулою:
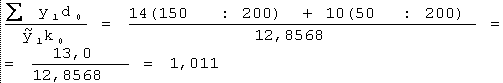
Цінність цього індексу, який отримується з щойно наведеної формули, полягає в тому, що він показує, наскільки сприятливою чи несприятливою виявилася б структура кількісного чинника базисного періоду при умові перенесення її в звітний період. Так, в нашому прикладі він свідчить про те, що структура посівів базисного періоду в умовах звітного виявилася б ефективнішою на 1,1 %, оскільки вона в більшій мірі відповідала б індивідуальним значенням врожайності звітного періоду, ніж базисного. Це пояснюється тим, що раніше більш урожайна культура (ячмінь) в звітному періоді по врожайності "відірвалася" від менш урожайної культури ще більше. Якби врожайність обох культур зростала в звітному періоді в порівнянні з базисним прямо пропорційно, такого ефекту не виявилося б. І навпаки, якби врожайність більш урожайної культури в звітному періоді збільшилася у відносно менших розмірах, індекс впливу структури посівів виявився б меншим одиниці.
Вплив другої частини структурного чинника зміни структури сукупності (посівних площ) на середню змінного складу розраховується за формулою:
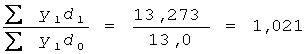
Цей індекс є аналогом традиційного індекса структурних зрушень, але зважений за рівнями врожайності не базисного, а звітного періоду, і в цьому полягає його незаперечна перевага.
Враховуючи розкладання індекса структурних зсувів на дві його складові, повний індекс середньої змінного складу в нашому прикладі буде таким:
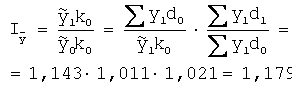
Викладений порядок агрегатного індексування може бути застосований до будь-якої середньої змінного складу. На основі приведених розрахунків визначаються і абсолютні прирости середньої змінного складу по чинниках, які в нашому прикладі складуть:
1) за рахунок зміни врожайності окремих культур:
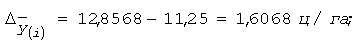
2) за рахунок впливу структури посівних площ базисного періоду на умови звітного періоду:
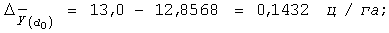
3) за рахунок змін у структурі посівних площ:
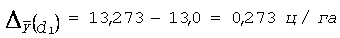
Таким чином, з точки зору підвищення достовірності результатів аналізу і розширення обсягу аналітичної інформації, викладене переконує в перевагах саме такого способу індексування середньої змінного складу. Розглянуті принципи такого аналізу можуть бути застосовані до різних якісних показників, динаміка яких вивчається зазвичай відомою системою індексів змінного складу.
Опубліковано : Андрієнко В.Ю. Cтатистичні індекси в економічних дослідженнях. – К. : 2004 р., с. 53 – 58.
