3.4.4. Closed systems and TSR postulates

V. I. Melnikov

The CS is, by definition, a system which experiences no external influence. The PB–PV system as a whole is a CS, since it possesses only internal interactions. Some parts of the PB–PV system can be not a CS because they can interact with each other. The IF is also a CS, as we have already established. To be more precise, it is a conditionally closed system (CCF). Therefore, the first TSR postulate follows from clauses 3 and 7 of the model.

The second TSR postulate, which implies that the speed of light is constant in any IF, can also be validated in the framework of our model and the above-described state of the PB–PV system. However, certain additional specifications are necessary.

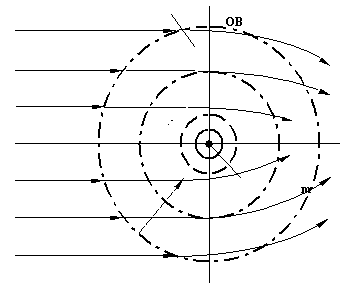
Fig. 13. The deflection of electromagnetic waves in the region of interaction between a mass and a physical vacuum: IR is the interaction region; a – increasing of the density of the optical ambience.

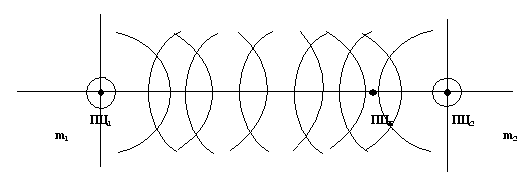
Fig. 14. The superposition of the regions of interaction of masses m₁ and m₂ and the formation of the resultant reduced interaction center RCΣ.

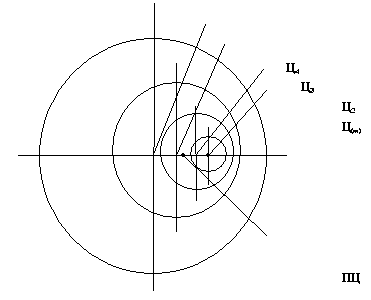
Fig. 15. The formation of the reduced interaction center in the case of accelerated motion: C₁, C₂ … C_n are the instantaneous interaction centers, RC is the reduced center.

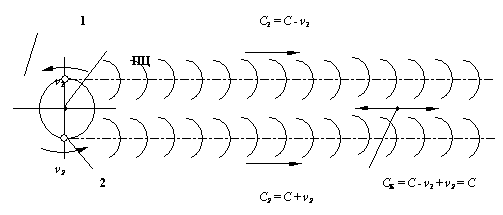
Fig. 16. The formation of the reduced reference center RC in the system "double stars–physical vacuum": ν₁ is the speed of light from the first star, ν₂ is the speed of light from the second star.

At first glance the second postulate seems to follow from the first postulate because the PB–PV system as a whole is a CS in which all the processes (including electromagnetic wave propagation) go on in the same manner. However, according to our model (see clause 2), the speed of light as the intensity Wij index is constant only for an optically homogeneous medium whose elements all have the equal level difference and the equal specific resistances of the isosurface belonging to the IL. This is the case of the internal (partial) CS in which the criterion of closure is secured by the cyclic equilibrium of the inertial magnetic and electric (capacitive) forces in association with the electromagnetic wave velocity. The equilibrium is described mathematically by the corresponding wave equation, or by the Maxwell equations in a more general case.

Thus, the wave equation describes the state of the local closed system and reflects the constancy of the optical medium parameters and, therefore, the constancy of electromagnetic wave velocity. So, the second TSR postulate (the constancy of the speed of light in any inertial frame) is transformed into the condition of the constancy of the speed of light in the region of any IR isosurface with a constant optical density. In this case the closed system of electromagnetic wave parameters (not the PB–PV system) manifests itself as the inertial frame.

We can draw the following analogy between the propositions of our model, the behavior of the PB–PV system, and some terms of the field theory.

Physical field – the region W_OB.

Field strength – specific intensity W_OB and accordingly specific mechanical power, referred to single condition PB, placed in this field

Potential in point of the field – a general energy of the interaction of the flow with single condition PB, residing in given to point.

Difference of potentials – the difference in the total energy of the flow between two points of the interaction region.

Gravitational and inertial forces – index of the region WOB asymmetry and index of the interaction flow asymmetry in different directions with respect to the PB.

Mass – index of the “mass” W_OB intensity.

In this case we can probably speak about the dynamical field model.

The following unified relations can be written after the generalization of the above-described partial cases to all kinds of interaction between the PB and the surrounding medium.

Equation of levels:

where ΔU_Σ is the difference between the levels of the general state of the PB and its medium; ΔU_m, ΔU_Э, ΔU_M are the level differences for the mass interaction, electric interaction, and magnetic interaction; ΔU_θ is the level difference which depends on velocity (e.g., due to viscous friction); ΔU_ij is the difference of levels (potentials) which depend on the starting point and finishing point of the trajectory of motion; and ΔU_X are the differences of other kind.

We can also write that

ΔU_m = ΔU_C + ΔU_T + ΔU_u

where ΔU_C is the spatially balanced (symmetric) level difference; ΔU_T is the level difference which gives birth to gravitational force, and ΔU_u is the level difference produced by the accelerated motion of the PB (it gives birth to inertial force).

The corresponding equation of intensities is

where I_m = I_C + I_T + I_u, and the index notation is the same as in Eq. (19).

The inertial frame corresponds to the case when ΔU_T + ΔU_u + ΔU_Э + ΔU_M + ΔU_θ + ΔU_ij + ΔU_X = 0, i.e., ΔU_Σ = ΔU_C, and, accordingly,

I_Σ = I_C = const

(or I_C >> I_T + I_u + I_Э + I_M + I_θ + I_ij + I_X). The intensity constancy means that there is no damping or the damping is ignored.

Hence the first TSR postulate is valid when I_Σ = I_C = const.

The second postulate refers to the electromagnetic wave propagation (rather than to the PB motion) with the cyclic (periodic) transition between IE and IM. In this case the total intensity remains constant in the local CS, i.e.,

I_Σ = I_Э + I_m = const.

Other terms in the right-hand side of Eq. are equal to zero.

Any physical object which is detected experimentally can be used as a PB in the framework of the proposed technique. In particular, elementary particles can be described in this way. This conclusion is based on the absence of the quantization of the generalized parameters in the TCS and in the generalized process. Moreover, the generators of the mass interaction and electric interaction are no more than 10^-58 and 10^-25 m in their size (Sect. 3.2). These dimensions are much smaller than the size of the elementary particles (including quarks) discovered directly or indirectly by now. The above-described interaction patterns are more significant for elementary particles in view of small distances and high specific intensities of interactions. Furthermore, our model opens up new possibilities for investigating the strong and weak interactions as well as for the novel interpretation of the well-known physical phenomena, e.g., the mass defect (Sect. 3.7).

The ideal interaction patterns in the PB–PV systems are much more complicated in the case of multi-body, multi-component, and multi-phase systems, including complex macro- and microsystems as well as cosmic systems. Since the electromagnetic and mass (gravitational) interactions have nearly infinite radii of action, their limiting velocities at any point are generally affected by the whole universe. So, the reduced reference frame is generally determined by the entire system of celestial bodies. The optical medium at the observation point is predominantly formed by the closest massive celestial bodies. Other parts of the universe exert some background action which never disappears completely. When there is no close massive body, the background frame turns into the reduced frame, which corresponds most closely to the hypothetic absolutely “motionless” aether (motionless with respect to the “motionless” system of stars).

Conclusions

Our hypothetic phenomenological concept for describing the physical objects and the generalized process of their interaction with the surrounding medium allowed us to resolve some TR inconsistencies and to propose the unified novel self-consistent qualitative interpretation of some existing physical phenomena and relevant experiments.

The model of the generalized physical process allows the TSR postulates and the “inertial frame” concept to be validated. Some properties and the origin of the medium (“aether”) in which electromagnetic oscillations propagate can also be justified.