3.4.4. Замкнутая система и постулаты СТО

Мельников В.И.

По определению ЗС – система, на которую не действуют никакие внешние воздействия. Поскольку система ФТ – ФВ взаимодействует только внутри себя, она в целом является ЗС. Отдельные части системы ФТ – ФВ могут не являться ЗС , т.к. между ними происходит процесс взаимодействия. Причем ИС, как мы видели выше, также будет являться ЗС, а точнее условно замкнутой системой (УЗС). Отсюда следует, что первый постулат СТО является следствием п.п. 3, 7 модели.

Второй постулат СТО, констатирующий постоянство скорости света в любой ИС, также может быть обоснован в рамках модели и описанного состояния системы ФТ – ФВ, но с определенными уточнениями.

Во-первых, поскольку система ФТ – ФВ в целом является ЗС, в которой все процессы протекают одинаково, то, казалось бы, это должно распространяться на процесс распространения электромагнитных волн во всей ЗС и этот постулат должен автоматически вытекать из первого. Но по модели (см. п. 2) постоянство скорости света, как показателю интенсивности W_ij, будет только в оптически однородной среде, все участки которой обладают равной разницей уровней и равными удельными сопротивлениями изоповерхности принадлежащей ЛВ. Т.е. это будет вариант внутренней (частной) ЗС, в которой критерий замкнутости будет обеспечен циклическим равновесием инерционных магнитных и емкостных электрических сил в сочетании с параметром скорости электромагнитной волны. Это равновесие математически описывается, как известно, соответствующим вариантом волнового уравнения, а в общем случае системой уравнений Максвелла.

Следовательно, в конечном итоге волновое уравнение описывает состояние локальной замкнутой системы, и отражает постоянство параметров оптической среды и, соответственно, постоянство скорости электромагнитных волн.

Следовательно, 2-й постулат СТО, констатирующий постоянство скорости света в любой инерциальной системе в представленной схеме трансформируется в условие постоянства скорости света в области какой-либо изоповерхности ЛВ, обладающей постоянной оптической плотностью. В качестве инерциальной системы в данном случае будет проявляться замкнутая система параметров электромагнитной волны, а не система ФТ – ФВ.

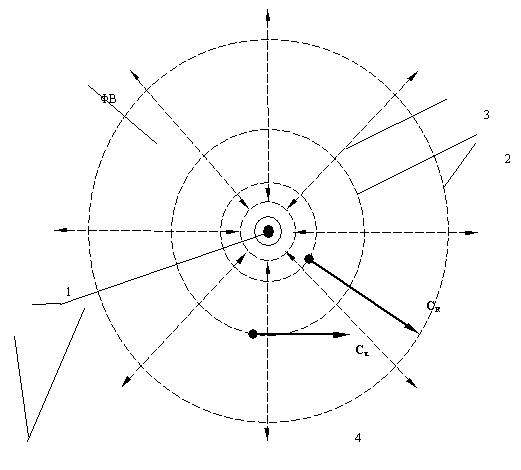
Рис. 12. Линза взаимодействия: 1 – ФТ; 2 – изоповерхности; 3 – направление потоков взаимодействия; 4 – траектории луча света C_τ – в тангенсальном направлении, С_R – в радиальном направлении.

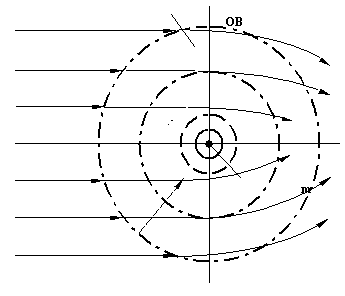
Рис. 13. Схема отклонения направления перемещения электромагнитных волн в области взаимодействия массы с физическим вакуумом: ОВ – область взаимодействия; повышение плотности оптической среды

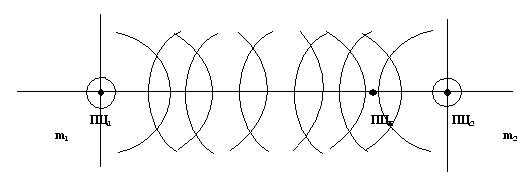
Рис. 14. Схема наложения областей взаимодействия масс m₁ и m₂ и образования суммарного приведенного центра взаимодействия ПЦΣ;

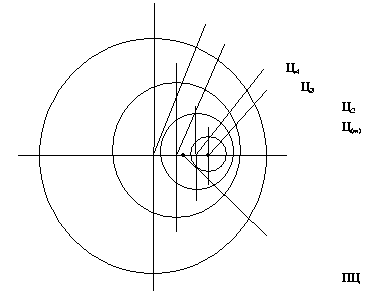
Рис. 15. Образование приведенного центра взаимодействия при ускоренном движении: Ц₁, Ц₂…Ц_n – мгновенные центры взаимодействия; ПЦ – приведенный центр.

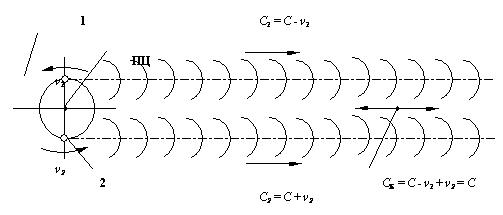
Рис. 16. Схема образования приведенного центра отсчета ПЦ в системе двойные звезды – физический вакуум: ν₁ – скорость света первой звезды; ν₂ – скорость света второй звезды.

Можно провести определенную аналогию между положениями модели, поведением системы ФТ – ФВ и некоторыми терминами теории поля.

Физическое поле – область W_OB.

Напряженность поля – удельная интенсивность W_OB и соответственно удельная механическая сила, отнесенная к единичному состоянию ФТ, помещенного в это поле.

Потенциал в точке поля – общая энергия взаимодействия потока с единичным состоянием ФТ, находящегося в данной точке.

Разность потенциалов – разница в общей энергии потока между двумя точками области взаимодействия.

Силы тяготения и инерции – показатели асимметрии области W_OB и соответственно, асимметрии потоков взаимодействия по направлениям относительно ФТ.

Масса – показатель интенсивности «массового» W_OB.

В данном случае вероятно можно говорить о динамической модели поля.

Обобщая приведенные частные случаи, на все виды взаимодействия ФТ с окружающей средой можно записать следующие комплексные зависимости.

Уравнение уровней.

где ΔU_Σ – разница уровней общего состояния ФТ и его среды; ΔU_m, ΔU_Э, ΔU_M – разница уровней соответственно для массового, электрического и магнитного взаимодействий; ΔU_θ – разница уровней, зависящая от скорости перемещения (например, при вязком трении); ΔU_ij – разница уровней (потенциалов), зависящих от начальной и конечной точек траектории движения; ΔU_X – прочие виды разницы уровней ФТ и его среды.

В свою очередь

ΔU_m = ΔU_C + ΔU_T + ΔU_u

где ΔU_C – пространственно уравновешенная (симметричная) разница уровней; ΔU_T – разница уровней, порождающая силы тяготения; ΔU_u – разница уровней, создаваемая ускоренным движением ФТ (вызывающая появление силы инерции).

Соответствующее уравнение интенсивностей

где I_m = I_C + I_T + I_u, и индексация интенсивностей соответствует индексации уравнения уровней (19).

Инерциальная система соответствует случаю, когда ΔU_T + ΔU_u + ΔU_Э + ΔU_M + ΔU_θ + ΔU_ij + ΔU_X = 0, т.е. ΔU_Σ = ΔU_C и соответственно

I_Σ = I_C = const

(или I_C >> I_T + I_u + I_Э + I_M + I_θ + I_ij + I_X). Постоянство интенсивностей означает, что затухания нет или им пренебрегаем.

Следовательно, первый постулат СТО имеет место, когда I_Σ = I_C = const.

Второй постулат соответствует случаю, когда перемещается не ФТ, а электромагнитная волна, т.е. реализуется циклический процесс, где происходит периодический переход I_Э в I_M и обратно, но сумма интенсивностей в локальной ЗС остается постоянной, т.е.

I_Σ = I_Э + I_m = const

Все остальные составляющие правой части уравнений равны нулю.

При использовании предлагаемой методики в качестве ФТ может рассматриваться любой из экспериментально обнаруживаемых в настоящее время физических объектов, включая элементарные частицы. Основанием для этого является, с одной стороны, отсутствие квантования обобщенных параметров в ТЗС и в обобщенном процессе, а с другой – полученные оценочные размеры генераторов массового и электрического взаимодействий находятся ниже размера соответственно 10^-58 и 10^-25 м (п. 3.2). Это значительно меньше размеров обнаруженных в настоящее время (непосредственно или косвенно) элементарных частиц, включая кварки. В мире элементарных частиц описанные схемы взаимодействия наиболее значимы из-за малых расстояний и соответственно высокой удельной интенсивности взаимодействий. Кроме того, появляются дополнительные возможности для исследования сильного и слабого взаимодействий и для новой интерпретации известных физических явлений, например, дефекта масс (п. 3.7).

Описанные простейшие идеальные схемы взаимодействия в системах ФТ – ФВ существенно усложняются при переходе к реальным многообъектным, многокомпонентным и многофазным системам, включая сложные системы макро- и микромира, а также космические системы. Учитывая практическую бесконечность радиусов действия электромагнитного и массового (гравитационного) взаимодействия их предельные скорости в общем случае в любой точке теоретически будут определяться всей Вселенной. И приведенная система отсчета в общем случае также будет определяться всей системой небесных тел. Близость какого-либо массивного небесного тела (или тел) к точке исследования будет, очевидно, играть определяющую роль в формировании оптической среды, а все остальные части Вселенной будут играть некоторую фоновую роль, не исчезал полностью никогда. При отсутствии близко расположенного массивного тела фоновая система отсчета превращается в приведенную систему, наиболее близко соответствующую гипотетическому абсолютно «неподвижному» эфиру, а точнее неподвижному относительно «неподвижной» системе звезд.

Выводы

Изложенная гипотетическая феноменологическая концепция представления физических объектов и их обобщенного процесса взаимодействия с окружающей средой позволяет снять ряд противоречий в современном состоянии ТО и дать единую принципиально новую комплексную непротиворечивую качественную интерпретацию ряда соответствующих физических явлений и результатов экспериментов.

Модель обобщенного физического процесса позволяет обосновать постулаты СТО и понятие «инерциальной системы».

Модель позволяет обосновать некоторые свойства и источник образования среды, в которой распространяются электромагнитные колебания («эфира»).