3.3. Силы инерции и притяжения – отталкивания
Мельников В.И.
В качестве примера применения предложенной модели рассмотрим некоторые аспекты поведения системы, состоящей из физического тела, обладающего массой (далее – масса) и окружающего массу физического вакуума, который при этом рассматривается как равноправный объект взаимодействия, т.к. он в соответствии с условием 1 обладает свойствами, отличными от свойств помещенной в него массы.
Вследствие очевидной разницы состояний массы и вакуума в соответствии с условием 1 между ними возникает некоторый гипотетический процесс взаимодействия, характеризуемый определенным потоком, перемещаемым между массой и вакуумом (условие 6). Кстати, активность физического вакуума и возможность вступления его во взаимодействие в настоящее время привлекают внимание многих физиков [7]. Вакуум уже не является полной пустотой, а представляет собой среду, заполненную бесконечным числом различных виртуальных частиц, порождающих квантовые флуктуации. По условию 2 критерием существования процесса является изменение экспериментально обнаруживаемых свойств вакуума вокруг массы, например, появление напряженности поля. Назовем условно это взаимодействие «массовым».
По условиям 2 и 14 свойства вакуума в процессе взаимодействия будут меняться, он перестанет быть вакуумом в собственном смысле этого слова и пространство вокруг массы будет заполнено какими-то продуктами взаимодействия. По условию 12 уровень взаимодействия пропорционален разнице масс тела и вакуума (пространства с продуктами взаимодействия или области взаимодействия), т.е. величине массы. Интенсивность (плотность) взаимодействия в изотропном пространстве по мере удаления от массы будет равномерно по всем направлениям уменьшаться по квадратичному закону из-за увеличения по тому же квадратичному закону нормального сечения потока в изотропном пространстве вокруг массы (кстати, понятие потока широко используется в теории поля как средство описания параметров поля и его зависимостей).
В случае наличия в потоке составляющей, вызывающей появление механических сил, их равнодействующая, приложенная к массе, будет равна нулю (рис. 9). При неоднородной (анизотропной, асимметричной) области взаимодействия вокруг массы последняя будет испытывать действие механической силы.
При этом безразлично, каким способом будет создана асимметрия: за счет несимметричности самой массы, помещения в пространство другой или других масс, наложения других видов взаимодействий, неравномерного движения массы (при конечной скорости потока взаимодействия) или каким-то иным способом.
Во всех случаях разница уровней по направлениям будет разная, соответственно (условие 12) будет различная интенсивность взаимодействия и неуравновешенность механических (и других) сил. Таким образом, силу тяготения и инерционную силу можно интерпретировать как частный случай проявления асимметричного «массового» взаимодействия. Аналогично можно проанализировать и системы, состоящие из электрических зарядов, намагниченных тел и окружающего пространства.
Результаты этого анализа позволяют выделить целую группу гипотетических процессов, представленных в нижней части табл. 3. При этом функциональное подобие соответствующих различных величин или их комплексов, расположенных по вертикали, сохраняется. Это процессы магнитного и электрического взаимодействия. Функцию инициирования будут выполнять параметры q1q2, J1J2, сопротивления ε0r2, μ0r2, изменения Fэс, FM, количественного накопления Fэсt, FMt, мощности KэсFэсq1q2, kMFMJ1J2, общей совершенной работы KэсFэсq1q2t, kMFMJ1J2t.
Приведенная модель позволяет также получить новую качественную и количественную интерпретацию известной эмпирической зависимости силы инерции, массы и ускорения (второй закон Ньютона). В этом случае по условию 12 и табл. 3 имеем:
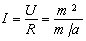
где I = Fин (сила инерции) – интенсивность; U = m2 – уровень; m/a – сопротивление R. (После подстановок получим то же, Fин = a · m).
Соответствующая новая качественная интерпретация выглядит следующим образом.
Ускоренно движущаяся масса создает асимметрию окружающей среды (области взаимодействия), величина которой пропорциональна величине массы m и ускорению a (рис. 7). Но масса m одновременно является и объектом, помещенным в эту же среду. Поэтому интенсивность I возникшего взаимодействия пропорциональна m2. Сопротивлению R соответствует комплекс m/a, т.к. та же масса m препятствует увеличению ускорения a, т.е. асимметрии области взаимодействия. Само ускорение a, в свою очередь, увеличивает асимметрию области взаимодействия, т.е. уменьшает сопротивление R и увеличивает интенсивность I. Масса m в этом случае выполняет, как видно, три функции.
Модель обобщенного процесса может быть использована при описании одномерных и двухмерных систем, хотя в настоящее время они изучены несравненно полнее, чем 3-мерные, как в теоретическом, так и в прикладном аспектах. Соответственно, менее вероятны и существенные корректировки в их понимании. Модель может быть использована также при анализе физических объектов и процессов других видов.
Использованная при описании процесса взаимодействия массы с физическим вакуумом терминология находится в прямом соответствии с терминологией общепринятого современного аппарата теории поля и некоторыми ее зависимостями (см. табл. 3).
В частности, очевидны следующие параллели:
Поле – область взаимодействия массы с физическим вакуумом (средой);
Напряженность в точке области – удельная интенсивность потока в области взаимодействия и соответственно удельная механическая сила, отнесенная к единичной массе;
Потенциал в точке поля – общая энергия взаимодействия потока с единичной массой, находящейся в данной точке;
Разность потенциалов – разница в общей энергии потока между двумя точками области взаимодействия;
Силы тяготения и инерции – величина асимметрии области взаимодействия и соответственно асимметрии интенсивности взаимодействия по направлениям;
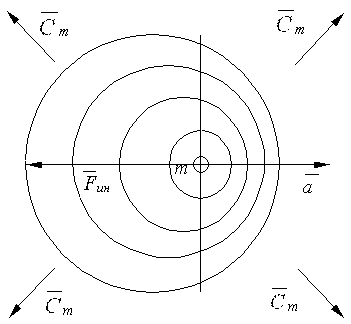
Рис.7. Деформация области взаимодействия при ускоренном движении
Масса – показатель интенсивности «массового» взаимодействия тела с окружающим физическим вакуумом (средой).
Это соответствие подтверждает правомерность существования рассматриваемой модели, расширяет представление о системе «масса – вакуум», а также говорит о возможности применения аппарата теории поля к исследованию этой системы.
В указанном соответствии отражается определенная динамическая модель физического поля.
В качестве примера правомерности последнего вывода рассмотрим гипотетический механизм возникновения силы инерции, возникающей, как известно, при неравномерном движении массы в пространстве. В соответствии с моделью инерция присуща ускоренному движению любого физического объекта, создающего асимметрию области взаимодействия, а сама асимметрия является следствием ускоренного движения объекта и конечности скорости распространения потока соответствующего вида взаимодействия (далее волна, фронт волны).
Для случая «массового» взаимодействия можно получить некоторые количественные зависимости. На рис. 8 приведена схема ускоренного прямолинейного движения массы и положения фронтов волн взаимодействия в различные моменты времени. При этом пространство предполагается однородным, а масса – точечной. Из точки О в момент времени t масса «излучает» волну взаимодействия, распространяющуюся с постоянной фазовой скоростью cm во всех направлениях относительно точек О и О1 (т.к. Δt -> 0, где Δt – время движения массы от точки О до точки О1). При этом использованы следующие обозначения: О – точка «излучения» фронта взаимодействия в момент времени t = 0; О1 – точка «излучения» фронта взаимодействия в момент времени (t + Δt); О2 – положение массы в момент времени t1, относительно которого определяется величина силы инерции; А, А1, В, В1 – положение фронтов волны взаимодействия при их движении по линии перемещения массы от точки О к точке О2 в момент времени t1; t1 – время перемещения массы из точки О в точку О2; (t1 – Δt) – время хода заднего фронта волны от точки О1 до точек В и В1 соответственно в прямом и обратном направлениях; Δt – также время хода волны от точек В и В1 соответственно до точек А и А1; 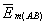 и
и 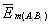 – усредненные векторы напряженности поля «массового» взаимодействия для интервалов АВ и А1В1; а – тангенциальное ускорение движения массы.
– усредненные векторы напряженности поля «массового» взаимодействия для интервалов АВ и А1В1; а – тангенциальное ускорение движения массы.
При исследовании используем общепринятый аппарат теории поля с соответствующими параметрами и обозначениями.
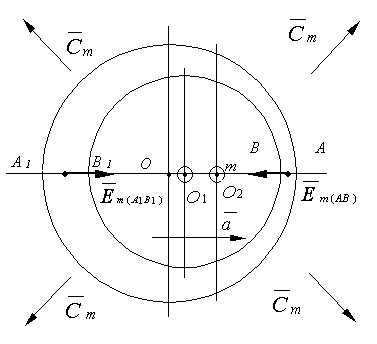
Рис. 8. Ход потоков взаимодействия при ускоренном движении
Рассмотрим величины векторов напряженности по направлению АА1 в интервалах АВ и А1В1; а. Градиент потенциала поля в этих интервалах вследствие малости Δt будем считать постоянным. Суммарная напряженность поля в направлении АА1
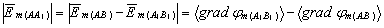 |
(18) |
где 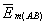 и
и 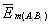 – усредненные векторы напряженности поля соответственно в интервалах АВ и А1В1;
– усредненные векторы напряженности поля соответственно в интервалах АВ и А1В1; 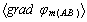 и
и 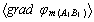 – усредненные градиенты потенциалов поля на соответствующих интервалах; φm – потенциал соответствующей точки поля.
– усредненные градиенты потенциалов поля на соответствующих интервалах; φm – потенциал соответствующей точки поля.
В свою очередь,
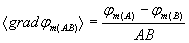 и
и 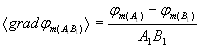 ,
,
где 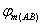 и
и 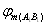 – средние потенциалы поля на интервалах АВ и А1В1.
– средние потенциалы поля на интервалах АВ и А1В1.
Значения потенциалов находим из следующих зависимостей:
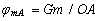 ;
; 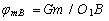 ;
;
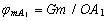 ;
; 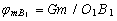 ,
,
где G – гравитационная постоянная; m – величина массы.
После соответствующих подстановок в уравнение (18), преобразований и исключения величин высшего порядка малости получим:
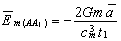
Для определения силы инерции необходимо найти векторы напряженности на поверхности элементарного генератора «излучения» (элементарной массы), а не всего физического тела, обладающего массой. Поэтому можем записать:
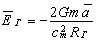
где Rr – эффективный радиус элементарного генератора «излучения», Rr = cmt1.
Сила, действующая со стороны поля на поверхность генератора, (сила инерции)
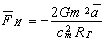
Знак минус в правой части уравнения означает, что сила инерции направлена в сторону, противоположную ускорению. Соответственно посторонняя сила, ускоряющая массу, совпадает по направлению с ускорением, т.е. посторонняя сила и сила инерции равны по величине и противоположны по направлению.
Напряженность поля обычно определяется в точке, размерами которой можно пренебречь, так же, как и радиусом кривизны соответствующей изолинии или изоповерхности поля (рис. 9). При исследовании действия на источник собственного поля, когда его размеры (размеры элементарной массы) сопоставимы с эффективным радиусом действия поля, такое пренебрежение недопустимо. Вместе с тем полностью отсутствуют экспериментальные данные о структуре переходной области между источником и полем. На данной стадии исследования это противоречие предполагается устранить введением специального коэффициента асимметрии, учитывающего искривление зоны «внутренней» границы поля, примыкающей к источнику, и соответствующим изменением направлений радиальных сил, действующих на источник со стороны поля. При этом уточняется некоторая суммарная напряженность поля по поверхности соответствующей полусферы источника (рис. 10). Очевидно, что при значительном удалении кa ~ 1, при максимальном приближении и минимальной деформации поля кa ~ 0,5. При значительной деформации поля ускоренным движением 0,5 < кa < 1.
Поэтому действительная суммарная сила действия поля на массу (сила инерции) будет равна
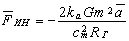
Таким образом, можно утверждать, что сила инерции является результатом действия на массу собственного поля, деформированного ее ускоренным движением.
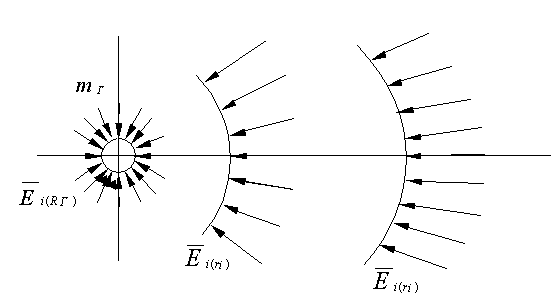
Рис. 9. Векторы напряженности поля в изотропном поле (без масштаба)
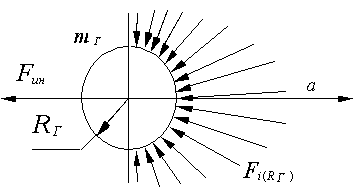
Рис. 10. Равнодействующие силы в переходной зоне; источник – поле в деформированном поле
Из опыта известно, что 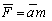 , поэтому после приравнивания аналитической и эмпирической сил инерции можем найти (точнее оценить) радиус генератора «излучения»
, поэтому после приравнивания аналитической и эмпирической сил инерции можем найти (точнее оценить) радиус генератора «излучения»
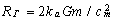
При оценке размеров генератора для большей точности необходимо брать минимальную из известных масс физических частиц.
Полученное выражение совпадает по форме с выражением гравитационного радиуса, впервые полученного Лейбницем и используемого в ОТО [113], но физический смысл его в данном случае совершенно иной.
Заметим, что приведенная методика исследования справедлива для источника любой природы, а также для определения силы тяготения (см. ниже).
Результаты численных расчетов значений Rr для «массового» и электромагнитного взаимодействия (протона и электрона) приведены в табл. 4. При этом предполагалось, что сm = с, где с – скорость света в вакууме, а кa = 0,6. Кстати, последние (2002 г.) измерения С. Копейкина и Э. Фламонта, проведенные с помощью исследования радиоизлучения квазара J0842 + 1835, проходящего через гравитационную линзу Юпитера, подтвердили, что 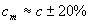 [30].
[30].
Таблица 4. Оценочные значения размеров генераторов гравитационного и электрического излучения для электрона и протона
| Объект | Исходные параметры | Радиус объекта, м | Rr, м | |||
| Заряд, Кл | Масса, кг | Скорость фронта, м/с | Коэффициенты кa | |||
| Электрон | 1,6·10-19 | 2,998·108 | 1/8,85·10-12 ф/м | 2,82·10-15 | 2,4·10-25 | |
| 9,1·10-31 | сm | 6,67·10-11 м3/кг·с2 | -«- | 7,74·10-58 | ||
| Протон | 1,6·10-19 | 2,998·108 | 1/8,85·10-12 ф/м | 0,7·10-15 | 2,4·10-25 | |
| 1,67·10-27 | сm | 6,67·10-11 м3/кг·с2 | -«- | 14,88·10-55 | ||
Анализ рассмотренного процесса «массового» взаимодействия и результатов расчетов позволяет сделать следующие выводы:
1. Поле тяготения и инерционное поле являются различными проявлениями одного процесса «массового» взаимодействия.
2. Величина массы является показателем интенсивности «массового» взаимодействия.
3. Сила инерции, возникающая при ускоренном движении массы, является результатом действия на нее собственного асимметричного поля, деформируемого ускоренным движением массы.
4. Размеры генераторов излучения рассмотренных полей намного порядков меньше размеров электрона и протона, что говорит о сложности их структуры.
5. Ввиду малых размеров генератора «массового» излучения и соответственно носителей излучения (гравитонов?) их экспериментальное обнаружение в ближайшей перспективе маловероятно.
6. Изменить силу инерции можно, изменяя параметры взаимодействия массы с окружающим пространством, например, наложением других полей на зону взаимодействия (например, полей других нуклонов ядра – эффект «дефекта» масс) (см. п. 3.7).
Существенные допущения, принятые при рассмотрении данного примера позволяют говорить лишь о грубой количественной оценке полученных величин, которые при более детальных исследованиях могут быть уточнены.
Асимметрия может быть создана с помощью наложения двух и более областей взаимодействия соответствующих источников (стоков) (рис. 11). В этом случае область вакуума, заключенная между источниками, в результате одновременного взаимодействия с несколькими источниками будет обладать состоянием, отличающимся от состояния внешних областей. Вследствие этого при их обратном действии на источник их равнодействующая не будет равна нулю и к последнему, в случае наличия в потоке механической составляющей, будет приложена механическая сила. Направление силы будет определяться видом и направлением потоков взаимодействия, в частности, типом возмущающего воздействия: источником, стоком или их определенной комбинацией.
Указанные рассуждения справедливы не только для гравитационного, электрического или магнитного взаимодействия и не только для трехмерного пространства. Аналогичная динамика должна наблюдаться и при других видах состояний и взаимодействий.
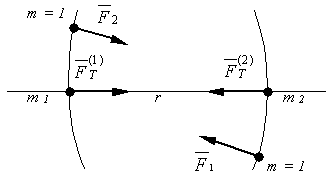
Рис. 11. Схема образования сил тяготения между двумя массами:
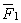 ,
, 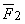 – силы, действующие на единичную массу со стороны соответственно m1 и m2;
– силы, действующие на единичную массу со стороны соответственно m1 и m2; 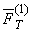 ,
, 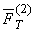 – силы тяготения, действующие соответственно на массу m1 со стороны m2 и на массу m2 со стороны m1
– силы тяготения, действующие соответственно на массу m1 со стороны m2 и на массу m2 со стороны m1
В настоящее время разработан достаточно совершенный математический аппарат для описания подобных систем. В частности, для 3-мерного случая систем с распределенными параметрами применяются линейные уравнения в частных производных Лапласа и Пуассона.
Для случая точечного объекта (заряда, массы, или другого источника или стока) во многих важных приложениях решения удобно находить с помощью функции его влияния (функции Грина) в неограниченном однородном пространстве, равной 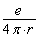 , где е – мощность источника, r – расстояние от точки влияния до источника. Эти уравнения и их решения, используемые в теории поля (в частности, потенциала), имеют важное значение в исследовании полей тяготения, магнито- и электростатики, диффузии, теплопроводности, несжимаемой жидкости и т.д., а в данном случае для определения величины силы, возникающей в асимметричной области взаимодействия.
, где е – мощность источника, r – расстояние от точки влияния до источника. Эти уравнения и их решения, используемые в теории поля (в частности, потенциала), имеют важное значение в исследовании полей тяготения, магнито- и электростатики, диффузии, теплопроводности, несжимаемой жидкости и т.д., а в данном случае для определения величины силы, возникающей в асимметричной области взаимодействия.
Градиент суммарного поля влияния в точке О2 (рис. 11), т.е. сила, действующая на единицу состояния объекта,
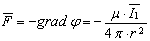
где r = O1O2; μ – коэффициент, учитывающий характер взаимодействия, свойства среды (области взаимодействия) и выбранной системы измерения; 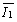 – интенсивность действия объекта О1 (величина заряда, массы).
– интенсивность действия объекта О1 (величина заряда, массы).
Общая сила (например, тяготения), действующая на объект О2 с интенсивностью действия 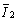 со стороны объекта О1,
со стороны объекта О1,
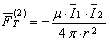
или аналогично
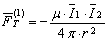
где 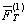 – сила, действующая на объект О1, обладающий интенсивностью
– сила, действующая на объект О1, обладающий интенсивностью 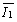 со стороны объекта О2, обладающего интенсивностью
со стороны объекта О2, обладающего интенсивностью 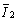 .
.
Эксперимент показывает, что для системы масса – вакуум – масса
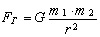
где G – гравитационная постоянная; m1, m2 – масса первого и второго объекта.
Отсюда
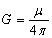
Аналогичное выражение получается, как известно, для случая электростатических зарядов или намагниченных тел.
При интерпретации объекта как источника несжимаемой жидкости справедливость приведенных результатов очевидна из-за разницы суммарных осевых реактивных сил в правом и левом полупространствах, возникающей из-за увеличенного сопротивления истечению жидкости со стороны соседнего источника.
Из вышесказанного также следует, что поскольку механизм действия асимметричной среды на сток или источник во всех случаях один и тот же, то силы инерции и тяготения будут возникать при любых видах взаимодействия, при условии наличия в потоке механической составляющей.
Из аналогичности этого механизма автоматически вытекает принцип эквивалентности инерционной и гравитационной масс, как разных форм проявления одного и того же вида массового взаимодействия.
