3.5. Скорость перемещения объектов в пространстве

Мельников В.И.

Скорость перемещения вместе с параметром величины перемещения и ускорения является одной из основных характеристик механического движения. Одновременно она является и одним из самых изученных и, казалось бы, самых простых физических параметров с физической, математической и технической точек зрения.

Менее исследован энергетический аспект параметра скорости и его зависимость от физической сущности перемещаемого объекта.

В обобщенных параметрах скорость перемещения является частным случаем интенсивности процесса взаимодействия:

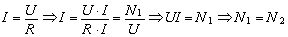(21)

где I – интенсивность; U – разница уровней состояний; R – сопротивление; N₁, N₂ – мощность, соответственно отводимая от перемещаемого объекта, и мощность, расходуемая на изменение антиобъекта – пути перемещения

N₁ = N₀ + N_вн

где N₀ – израсходованная внутренняя энергия перемещаемого объекта; N_вн – подводимая к объекту внешняя энергия.

В традиционных параметрах равномерного прямолинейного механического движения при встречной силе сопротивления (например, силе трения) получим

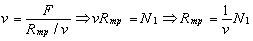
где v – скорость движения; F – внешняя сила, обеспечивающая движение; R_тр – сила трения; N₁ – мощность, подводимая к движущемуся телу.

В последнем выражении величина 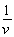является коэффициентом пропорциональности между мощностью N₁ и силой сопротивления R_тр. При увеличении скорости v и сохранении неизменным подводимой мощности N₁ сила сопротивления должна уменьшиться и наоборот, т.е. отношение 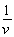является показателем величины сопротивления среды перемещению. Для фиксации этого важного момента обозначим

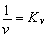
и запишем соответственно

R_тр = K_ν;N₁.

Аналогично в соответствии с (21) для обобщенного процесса можем записать

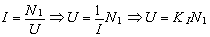(22)

где K_I – коэффициент пропорциональности между подводимой к измененному объекту мощностью и уровнем сопротивления процессу изменения.

Рассмотрим, является ли структура этой зависимости общей для любого частного процесса перемещения, например, волнового процесса. Если рассмотреть с учетом зависимости (22) процесс распространения волны, то можно показать, что общеизвестное одномерное волновое уравнение

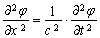
по своей структуре соответствует выражению, описывающему обобщенный процесс. Для этого представим это уравнение в виде системы двух уравнений

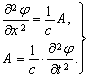(23)

Частная производная 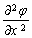представляет собой удельный градиент скалярного потенциала сплошной среды, а производная 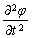является удельной скоростью изменения этого потенциала во времени. Для случая звуковых волн производная 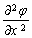интерпретируется как удельное напряжение, а 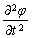– как удельная скорость изменения напряжения во времени. Параметр A для обоих уравнений (23) имеет размерность мощности, т.е. 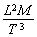, а частная производная 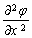имеет размерности силы (ньютон), т.е. первое уравнение преобразуется к виду

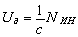
где U_a – уровень (величина) деформирующей силы; N_ИН – мощность, развиваемая силами инерции.

Во втором уравнении размерность скалярного потенциала

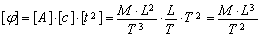
отсюда размерность

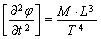
После подстановки этих размерных комплексов в уравнение (23) получим:

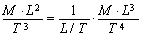
или

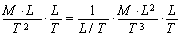
После сокращения получим

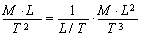
или

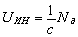
где U_ИН – уровень (величина силы инерции); N_d – мощность, развиваемая деформирующей силой.

Таким образом, исходное волновое уравнение для случая звуковых волн преобразуется в два частных уравнения описывающих соответственно процессы

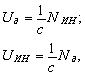
преобразования силы инерции в силу деформации и преобразование силы деформации упругой среды в силу инерции. Следовательно, волновое уравнение для случая звуковых волн является частным случаем обобщенного уравнения механического движения (22). Параметр 1/c в частном и обобщенном случаях является коэффициентом пропорциональности между мощностью потока внешнего воздействия на движущийся объект (волну) и силой реакции объекта на это воздействие.

Волновое уравнение, описывающее процесс распространения электромагнитных волн, также может быть приведено к виду обобщенного уравнения (22). В этом случае речь идет о поперечных колебаниях, описываемых скаляром φ и векторами A, E, и H [116]. Все эти величины (векторы в форме проекций на оси прямоугольной декартовой системы координат) для трехмерного случая удовлетворяют волновому уравнению:

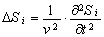, (i = 0…10)

где Δ – оператор Лапласа; 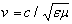– фазовая скорость электромагнитной волны; 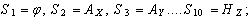; ε и μ – относительные диэлектрическая и магнитная проницаемости среды.

Следовательно, в общем случае эту систему можно преобразовать в систему 20 уравнений, каждое из которых будет аналогично обобщенному уравнению (22). К обобщенному уравнению вида (22) легко могут быть преобразованы любые физические зависимости, содержащие электродинамическую постоянную c.

Например, зависимость E = mc² также преобразуется к виду (22):

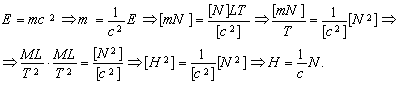
Аналогично преобразуется зависимость

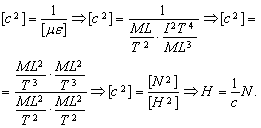
Можно привести ряд других аналогичных примеров с преобразованием уравнений, содержащих c.

Следовательно, процесс распространения электромагнитных волн в пространстве является частным случаем обобщенного перемещения и поэтому его можно считать рядовым физическим процессом, так же как и его параметры.

Таким образом, можно утверждать, что приведенное обобщенное уравнение (29) является базовым для описания перемещения в пространстве объектов любой природы, и оно может быть использовано при описании и исследовании любых процессов, связанных с перемещением объектов различной природы в пространстве.